若f″(x)不变号,且曲线y=f(x)在点(1,1)上的曲率圆为x2+y2=2,则函数f(x)在区间(1,2)内( )。
由题意可知,f(x)是一个凸函数,即f″(x)<0,且在点(1,1)处的曲率
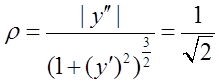
而f′(1)=-1,由此可得,f″(1)=-2。在[1,2]上,f′(x)≤f′(1)=-1<0,即f(x)单调减少,没有极值点。对于f(2)-f(1)=f′(ξ)<-1,ξ∈(1,2)(拉格朗日中值定理)。
又因为f(1)=1>0,且f(2)-f(1)<-1,所以f(2)<0,由零点定理知,在[1,2]上,f(x)有零点。故应选B项。