当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->2021年教师资格证考试《数学学科知识与教学能力》(高级中学)名师预测卷4
若1+√2i是关于χ的实系数方程χ2+bχ+c=0的一个复数根,则( )。
《普通高中数学课程标准(实验)》设置了四个选修系列,其中选修系列l是为希望在人文社会科学等方面发展学生而设置的,下列内容不属于选修系列1的是( )。
对高中数学的评价,下列说法错误的是( )。
已知命题p: χ1,χ2∈R,(f(χ2)-f(χ1))(χ2-χ1)≥O,则 p是( )。 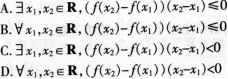
结合教学实际说一说.你认为新课程标准对教师的课堂教学有哪些要求

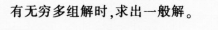
对数学概念教学的认识与提高应从哪几方面入手
简述中学数学思想方法的教学原则中的系统性原则。
高中课程的基本理念有哪些
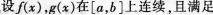
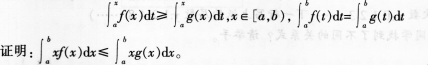
谈谈你理解的合作学习中的同质分组和异质分组。
案例:下面是一道鸡兔同笼问题:
一群小兔一群鸡,两群合到一群里,要数腿共48,要数脑袋整l7,多少小兔多少鸡
解法一:用算术方法:
思路:如果没有小兔,那么小鸡为17只,总的腿数应为34条,但现在有48条腿,造成腿的数目不够是由于小兔的数目是O,每有一只小兔便会增加两条腿,敌应有(48—17×2)÷2=7只小兔。相应地,小鸡有10只。
解法二:用代数方法:
可设有x只小鸡,y只小兔,则x+y=17①;2x+4y=48②。
将第一个方程的两边同乘以-2加到第二个方程中去,得x+y=17;(4-2)y=48-17x2。
解上述第二个方程得y=7,把y=7代入第一个方程得x=10。
所以有10只小鸡.7只小兔。
问题:
(1)试说明这两种解法所体现的算法思想;(10分)
(2)试说明这两种算法的共同点。(10分)
请以“直线与平面平行的判定”为课题,完成下列教学设计。
(1)教学目标(10分)
(2)本节课的教学重、难点(10分)
(3)写出新课引入和新知探究、巩固、应用等及设计意图(10分)