某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:

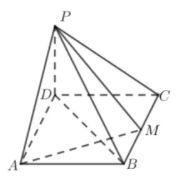
如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM
(1)证明:平面PAM⊥平面PBD
(2)若PD= DC=1 ,求四棱锥P- ABCD的体积.

已知抛物线C :y²=2 px( p>0)的焦点F到准线的距离为2.
(1)求C的方程;


已知函数f(x)=x³-x² + ax +1.
(1)讨论f(x)的单调性;
(2)求曲线y=f(x)过坐标原点的切线与曲线y= f(x)的公共点的坐标.
在直角坐标xOy 中,⊙C的圆心为C(2,1),半径为1.
(1)写出⊙C的一个参数方程;
(2)过点F(4,1)作⊙C的两条切线.以坐标原点为极点,r正半轴为极轴建立极坐标系,求这两条切线的极坐标方程.
己知函数f(x)=|x-a|+|x+3|
(1)当a=1时,求不等式f(x)≥6的解集;
(2)若f(x) >—a,求a的取值范围.