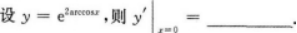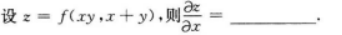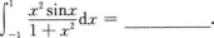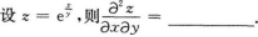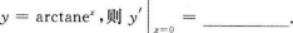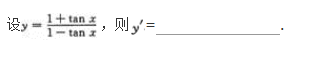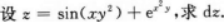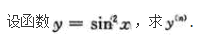当前位置：首页 → 学历类 → 成考（专升本） → 高等数学二（专升本）->2022年成人高等考试《高等数学二》（专升本）预测试卷
如果在区间(a，b)内，函数f(x)满足f′(x)>0，f′′(x)<0，则函数在此区间是()
某建筑物按设计要求使用寿命超过50年的概率为0．8，超过60年的概率为0．6，该建筑物经历了50年后，它将在10年内倒塌的概率等于()
设F(z)是f(z)的一个原函数，则∫cosxf(sinx)dx=（ ）
甲、乙两人独立地对同一目标射击一次，其命中率分别为0．6和0．5，现已知目标被命中，是甲射中的概率为（ ）
用A表示事件“甲考核通过且乙考核不通过”，则其对立事件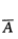
为（ ）
一批零件中有10个合格品，3个次品，安装机器时，从这批零件中任取一个，取到合格品才能安装．若取出的是次品，则不再放回，求在取得合格品前已取出的次品数X的概率分布．
一个袋子中有5个球，编号为1，2，3，4，5，同时从中任取3个，以X表示取出的3个球中的最大号码，求随机变量X的概率分布.
曲线x2+y2=2x在点(1，1)处的切线方程为.
曲线y=x3-3x2+2x+1的拐点是
∫sin2xCosxdx=.
求y=f(x)=2x3-3x2-12x+14的极值点和极值，以及函数曲线的凸凹性区间和拐点.
当x>0时，证明：ex>1+x.
设y=x2cosx+2x+e，则y′=．
设y=Incosx，求y′′(0)．
从一批有10件正品及2件次品的产品中，不放回地一件一件地抽取产品，设每个产品被抽到的可能性相同，求直到取出正品为止所需抽取的次数X的概率分布。
确定函数y=2x4-12x2的单调区间、极值及函数曲线的凸凹性区间和拐点．
求曲线y=x2与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积．
求由方程2x2+y2+z2+2xy-2x-2y-4z+4=0确定的隐函数的全微分．
设曲线y=x2+x-2在点M处切线的斜率为2，则点M的坐标为（）.
电路由两个并联电池A与B，再与电池C串联而成，设电池A、B、C损坏的概率分别是0.2，0.2，0.3，求电路发生间断的概率．
求曲线y=x2，与该曲线在x=a(a>o)处的切线与x轴所围的平面图形的面积．
求函数y=2x3-3x2的单调区间、极值及函数曲线的凸凹性区间、拐点和渐近线．
求一个正弦曲线与x轴所围成图形的面积.（只计算一个周期的面积）.
二元函数z=xy在x+y=1下的极值为___________.
设工厂A到铁路线距离为20公里，垂足为B，铁路线上距离B为100公里处有一原料供应站C，现从BC间某处D向工厂A修一条公路，为使从C运货到A运费最省，问D应选在何处？（已知每公里铁路与公路运费之比为3:5）
一批零件中有10个合格品和2个废品，安装机器时，从这批零件中任取一个，如果每次取出废品后不再放回，用X表示在取得合格品以前已取出的废品数，求：
1.随机变量X的分布列；
2.随机变量X的分布函数.
（1）求在区间[0，π]上的曲线y=sinx与x轴所围成图形的面积S.
（2）求（1）中的平面图形绕x轴旋转一周所得旋转体的体积V.
设f(x)是[-2，2]上的偶函数，且f′(-1)=3，则f′(1)．
有拐点(1，-1)．
令y'=0，得x=0；当x>0时．y'>0；当x<0时，y’<0，故在(-1，1)内，函数有增有减．
【考情点拨】本题考查了不定积分的知识点
所以y''(0)=-1．
应用的知识点．
【考情点拨】本题考查了一元函数在一点处的一阶导数的知识点．
【考情点拨】本题考查了隐函数在一点处的一阶导数的知识点．
【考情点拨】本题考查了不定积分的知识点．
【考情点拨】本题考查了二元函数的混合偏导数的知识点．
【考情点拨】本题考查了二元函数的一阶偏导数的知识点．
【考情点拨】本题考查了二元函数的混合偏导数的知识点．
【考情点拨】本题考查了不定积分的知识点．
【考情点拨】本题考查了定积分的知识点．
-sin(xy2)·(xy2)'=-2xysin(xy2)．
注：本题也可用洛必达法则求解．
=∫(sinx+Cosx)dx
注：将分母sin2x用于之等价的无穷小量x2代
