当前位置:首页 → 学历类 → 成考(专升本) → 高等数学二(专升本)->2022年成人高等考试《高等数学二》(专升本)押题密卷
函数y=ax2+c在(0,+∞)上单调增加,则a,c应满足【】
如果在区间(a,b)内,函数f(x)满足f'(x)>0,f''(x)<0,则函数在此区间是( )
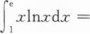
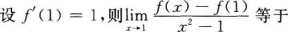 ( )
( )
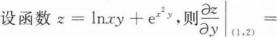
从1到10这十个正整数中任取一数,取得奇数的概率为___________.
甲袋中有15只乒乓球,其中3只白球,7只红球,5只黄球,乙袋中有20只乒乓球,其中10只白球,6只红球,4只黄球.现从两袋中各取一只球,求两球颜色相同的概率.
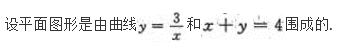
1.求此平面图形的面积S.

甲乙两人独立地向同一目标射击,甲乙两人击中目标的概率分别为0.8与0.5,两人各射击一次,求至少有一人击中目标的概率.

1.切点A的坐标;
2.过切点A的切线方程;
3.由上述曲线和切线及x轴所围成的平面图形绕x轴旋转一周所成旋转体的体积.
一批零件中有10个合格品,3个次品,安装机器时,从这批零件中任取一个,取到合格品才能安装.若取出的是次品,则不再放回,求在取得合格品前已取出的次品数X的概率分布.
求由方程2x2+y2+z2+2xy-2x-2y-4z+4=0确定的隐函数的全微分.
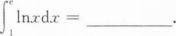

设y=x2cosx+2x+e,则y'=________.
设y=excosx,则y”=______.
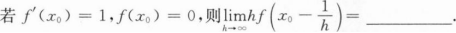
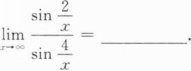

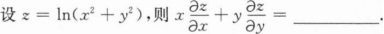
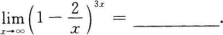
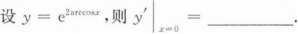
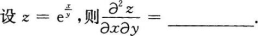
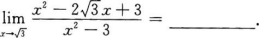
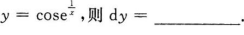
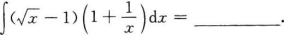
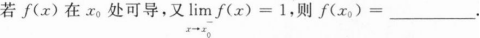
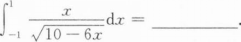
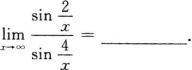
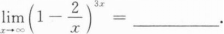
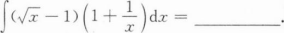
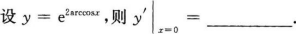
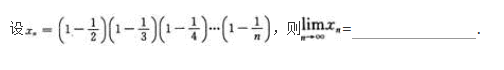
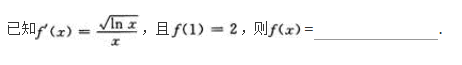

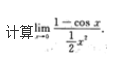
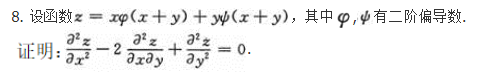




确定函数y=2x4—12x2的单调区间、极值及函数曲线的凸凹性区间和拐点.
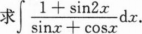
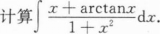
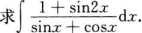

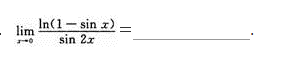


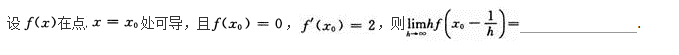
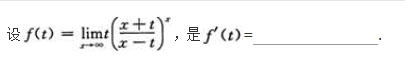

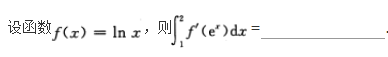

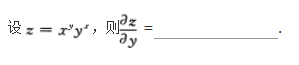
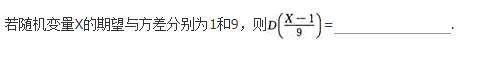
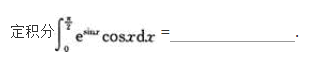
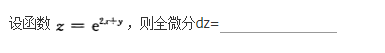
求函数y=2x3—3x2的单调区间、极值及函数曲线的凸凹性区间、拐点和渐近线.


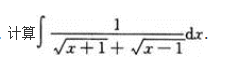
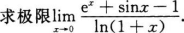
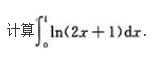

一个袋子中有5个球,编号为1,2,3,4,5,同时从中任取3个,以X表示取出的3个球中的最大号码,求随机变量X的概率分布.
设y=lncosx,求y''(0).
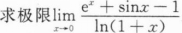

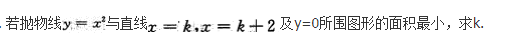
当x>0时,证明:ex>1+x.
证明:2x>x2(x>4).
