设函数z＝z（x，y）由方程F（y/x，z/x）＝0确定，其中F为可微函数，且F2′≠0，则x·（?z/?x）＋y·（?z/?y）＝（ ）。
设y1，y2是一阶线性非齐次微分方程y′＋p（x）y＝q（x）的两个特解，若常数λ，μ使λy1＋μy2是该方程的解，λy1－μy2是该方程对应的齐次方程的解，则（ ）。
设向量组Ⅰ：α1，α2，…，αr可由向量组Ⅱ：β1，β2，…，βs线性表示，下列命题正确的是（ ）。
求函数
的单调区间与极值.
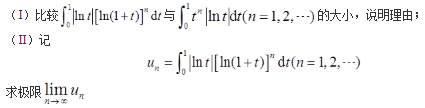
设函数y＝f（x）由参数方程
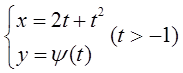
所确定，其中ψ（t）具有2阶导数，且ψ（1）＝5/2，ψ′（1）＝6，已知
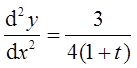
求函数ψ（t）。
一个高为l的柱体形贮油罐，底面是长轴为2a，短轴为2b的椭圆。现将贮油罐平放，当油罐中油面高度为3b/2时，计算油的质量。（长度单位为m，质量单位为kg，油的密度为常数ρkg/m3）
计算二重积分
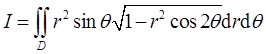
其中D＝{（r，θ）∣0≤r≤secθ，0≤θ≤π/4}。
设函数f（x）在闭区间[0，1]上连续，在开区间（0，1）内可导，且f（0）＝0，f（1）＝1/3，证明：存在ξ∈（0，1/2），η∈（1/2，1），使得f′（ξ）＋f′（η）＝ξ2＋η2。
设
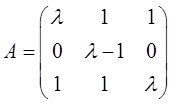
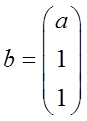
已知线性方程组Ax＝b存在2个不同的解。
（Ⅰ）求λ、a；
（Ⅱ）求方程组Ax＝b的通解。
设
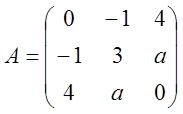
正交矩阵Q使得QTAQ为对角矩阵，若Q的第一列为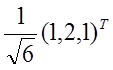
，求a、Q。
的收敛性（ ）。
进行讨论：被积函数只在x→0＋时无界。因为
收敛，所以
收敛。
进行讨论：被积函数只在x→1－时无界。因为
收敛，所以
收敛。
都收敛，故选D。
