已知平面区域D={(x,y)∣∣x∣+∣y∣≤π/2},记
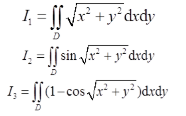
则( )。
曲线y=xsinx+2cosx(-π/2<x<2π)的拐点是( )。
设函数f(x),g(x)的2阶导函数在x=a处连续,则
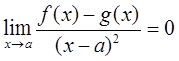
是两条曲线y=f(x),y=g(x)在x=a对应的点处相切及曲率相等的( )。
求不定积分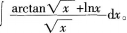
已知函数
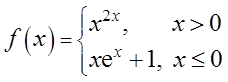
求f′(x),并求f(x)的极值。
设函数y(x)是微分方程
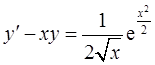
满足条件
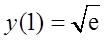
的特解。
(Ⅰ)求y(x);
(Ⅱ)设平面区域D={(x,y)|1≤x≤2,0≤y≤y(x)},求D绕x轴旋转所得旋转体的体积。
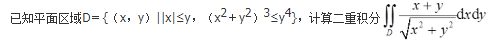
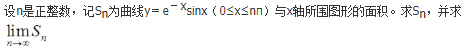
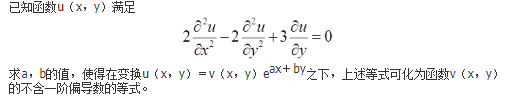
已知函数f(x)在[0,1]上具有2阶导数,且f(0)=0,f(1)=1,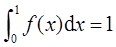 ,证明:
,证明:
(Ⅰ)存在ξ∈(0,1),使得f′(ξ)=0;
(Ⅱ)存在η∈(0,1),使得f″(η)<-2。

