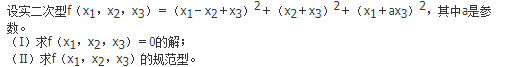设函数f(x)在[0,1]上二阶可导,且
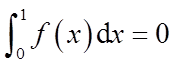
则( )。
设A、B为n阶矩阵,记r(X)为矩阵X的秩,(X,Y)表示分块矩阵,则( )。
求不定积分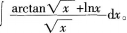
将长为2m的钢丝分为三段,依次围成成圆、正方形和正三角形,三个图形的面积之和是否存在最小值若存在,求出最小值。
数列{xn},x1>0,
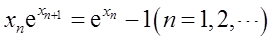
证明{xn}收敛,并求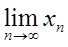
已知常数k≥ln2-1,证明:(x-1)(x-ln2x+2klnx-1)≥0。
已知连续函数f(x)满足
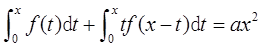
(Ⅰ)求f(x);
(Ⅱ)若f(x)在区间[0,1]上的平均值为1,求a的值。
设平面区域D由曲线
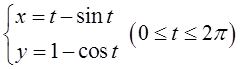
与x轴围成,计算二重积分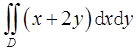
已知曲线L:y=4x2/9(x≥0),点O(0,0),点A(0,1),设P是L上的动点,S是直线OA与直线AP及曲线L所围成图形的面积,若P运动到点(3,4)时沿x轴正向的速度是4,求此时S关于时间t的变化率。