设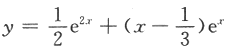
是二阶常系数非齐次线性微分方程
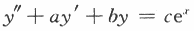的一个特解，则
设函数f(x)=x+aln(1+x)+bxsinx，g(x)=kx^3，若f(x)与g(x)在x→0是等价无穷小，求a，b，k值.
设函数f(x)在定义域I上的导数大于零，若对任意的x0∈I，曲线y=f(x)在点(x0，f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4，且f(0)=2，求f(x)的表达式.
已知函数f(x，y)=x+y+xy，曲线C：x^2+y^2+xy=3，求f(x，y)在曲线C上的最大方向导数.
(Ⅰ)设函数u(x)，ν(x)可导，利用导数定义证明［u(x)ν(x)］’=u’(x)ν(x)+u(x)ν’(x)；
(Ⅱ)设函数u1(x)，u2(x)，…，un(x)可导，f(x)=u1(x)u2(x)…un(x)，写出f(x)的求导公式.
设随机变量X的概率密度为
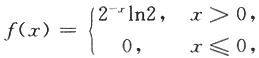
对X进行独立重复的观测，直到第2个大于3的观测值出现时停止，记Y为观测次数.
(Ⅰ)求Y的概率分布；
(Ⅱ)求EY.
设总体X的概率密度为
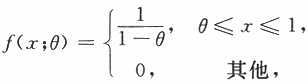
其中θ为未知参数，X1，X2，…，Xn，为来自该总体的简单随机样本.
(Ⅰ)求θ的矩估计量；
(Ⅱ)求θ的最大似然估计量.
确定，则
=_________.
=_________.
中，f(x，y)在曲线C上的最大方向导数为3.
