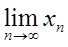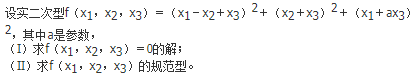设某产品的成本函数C(Q)可导,其中Q为产量,若产量为Q0时平均成本最小,则( )。

设函数f(x)在[0,1]上二阶可导,且
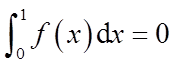
则( )。
设A、B为n阶矩阵,记r(X)为矩阵X的秩,(X,Y)表示分块矩阵,则( )。
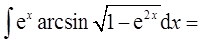
设A为3阶矩阵,α1,α2,α3为线性无关的向量组。若Aα1=α1+α2,Aα2=α2+α3,Aα3=α1+α3,则|A|=

差分方程Δ2yx-yx=5的通解为
已知实数a、b满足
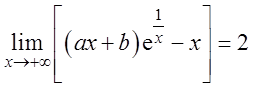
求a,b。
已知a是常数,且矩阵
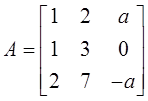
可经初等列变换化为矩阵
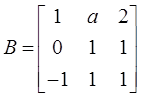
(Ⅰ)求a;
(Ⅱ)求满足AP=B的可逆矩阵P。
设随机变量X与Y相互独立,X的概率分布为P{X=1}=P{X=-1}=1/2,Y服从参数为λ的泊松分布,令Z=XY。
(Ⅰ)求Cov(X,Z);
(Ⅱ)求Z的概率分布。

将长为2m的钢丝分为三段,依次围成成圆、正方形和正三角形,三个图形的面积之和是否存在最小值若存在,求出最小值。
已知
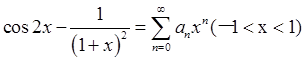
求an。
数列{xn},x1>0,
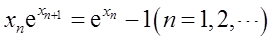
证明{xn}收敛,并求