计算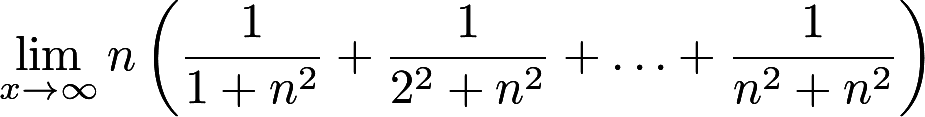
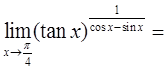
设随机变量X和Y相互独立,且均服从参数为1的指数分布,V=min(X,Y),U=max(X,Y)。求:
(Ⅰ)随机变量V的概率密度fV(v);
(Ⅱ)E(U+V)。
某企业为生产甲、乙两种型号的产品投入的固定成本为10000(万元),设该企业生产甲、乙两种产品的产量分别为x(件)和y(件),且这两种产品的边际成本分别为20+x/2(万元/件)与6+y(万元/件)。
(Ⅰ)求生产甲、乙两种产品的总成本函数C(x,y)(万元);
(Ⅱ)当总产量为50件时,甲、乙两种产品的产量各为多少时可使总成本最小求最小成本;
(Ⅲ)求总产量为50件且总成本最小时甲产品的边际成本,并解释其经济意义。

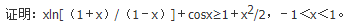
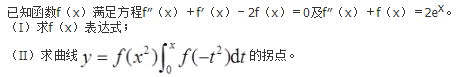
设
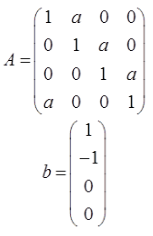
(Ⅰ)求|A|;
(Ⅱ)当实数a为何值时,方程组Ax=b有无穷多解,并求其通解。

设二维离散型随机变量(X,Y)的概率分布如表1所示。
表1
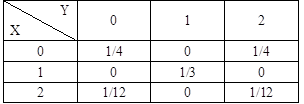
求:
(Ⅰ)P{X=2Y};
(Ⅱ)Cov(X-Y,Y)。