当前位置：首页 → 学历类 → 高考 → 数学（文科）->2022年安徽省芜湖市高考文科数学押题试卷

2022年安徽省芜湖市高考文科数学押题试卷

卷面总分：23分 答题时间：240分钟 试卷题量：23题 练习次数：118次
单选题 （共12题，共12分）
1.

设集合 M＝{x|0＜x＜4}， N＝{x| 1/3≤x≤5}， 则 M∩ N＝（）

  • A. {x|0＜x≤1/3 }
  • B. {x| 1/3≤x＜4}
  • C. {x|4≤x＜5}
  • D. {x|0＜x≤5}
标记 纠错
2.

为了解某地农村经济情况， 对该地农户家庭年收入进行抽样调查， 将农户家庭年收入的调查数据整理得到如下频率分布直方图：

image.png

根据此频率分布直方图， 下面结论中不正确的是（）

  • A. 该地农户家庭年收入低于 4.5 万元的农户比率估计为 6%
  • B. 该地农户家庭年收入不低于 10.5 万元的农户比率估计为 10%
  • C. 估计该地农户家庭年收入的平均值不超过 6.5 万元
  • D. 估计该地有一半以上的农户， 其家庭年收入介于 4.5 万元至 8.5 万元之间
标记 纠错
3.

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
4.

青少年视力是社会普遍关注的问题， 视力情况可借助视力表测量． 通常用五分记录法和小数记录法记录视力数据， 五分记录法的数据 L 和小数记录法的数据 V满足 L＝5+lgV． 已知某同学视力的五分记录法的数据为 4.9， 则其视力的小数记录法的数据约为（）image.png

  • A. 1.5
  • B. 1.2
  • C. 0.8
  • D. 0.6
标记 纠错
5.

已知 F 1 ， F 2 是双曲线 C 的两个焦点， P 为 C 上一点， 且∠F 1 PF 2 ＝60° ， |PF 1 |＝3|PF 2 |，则 C 的离心率为（）

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
6.

如图， 在一个正方体内放入两个半径不相等的球 O 1 、 O 2 ， 这两个球相外切， 且球 O 1 与正方体共顶点 A 的三个面相切， 球 O 2 与正方体共顶点 B 1 的三个面相切， 则两球在正方体的面 AA 1 C 1 C 上的正投影是（）

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
7.

等比数列{a n }的公比为 q， 前 n 项和为 S n ． 设甲： q＞0， 乙： {S n }是递增数列， 则（）

  • A. 甲是乙的充分条件但不是必要条件
  • B. 甲是乙的必要条件但不是充分条件
  • C. 甲是乙的充要条件
  • D. 甲既不是乙的充分条件也不是乙的必要条件
标记 纠错
8.

2020 年 12 月 8 日， 中国和尼泊尔联合公布珠穆朗玛峰最新高程为 8848.86（单位： m），三角高程测量法是珠峰高程测量方法之一． 如图是三角高程测量法的一个示意图， 现有 A，B， C 三点， 且 A， B， C 在同一水平面上的投影 A'， B'， C'满足∠A'C'B'＝45° ， ∠A'B'C'＝60° ． 由 C 点测得 B 点的仰角为 15° ， BB'与 CC'的差为 100； 由 B 点测得 A 点的仰角为 45° ， 则 A， C 两点到水平面 A'B'C'的高度差 AA'﹣ CC'约为（）（√3 ≈1.732）

image.png

  • A. 346
  • B. 373
  • C. 446
  • D. 473
标记 纠错
9.

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
10.

将 4 个 1 和 2 个 0 随机排成一行， 则 2 个 0 不相邻的概率为（）

  • A. 1/3
  • B. 2/5
  • C. 2/3
  • D. 4/5
标记 纠错
11.

已知 A， B， C 是半径为 1 的球 O 的球面上的三个点， 且 AC⊥BC， AC＝BC＝1， 则三棱锥 O﹣ ABC 的体积为（）

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
12.

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
填空题 （共4题，共4分）
13.

image.png

标记 纠错
14.

image.png

标记 纠错
15.

image.png

标记 纠错
16.

image.png

标记 纠错
问答题 （共7题，共7分）
17.

近几年， 随着大众鲜花消费习惯的转变， 中国进入一个鲜花消费的增长期． 根据以往统计， 某地一鲜花店销售某种 B 级玫瑰花， 在连续统计的 320 天的玫瑰花售卖中，每天的玫瑰花的销售量（单位： 支） 与特殊节日的天数如表：

image.png

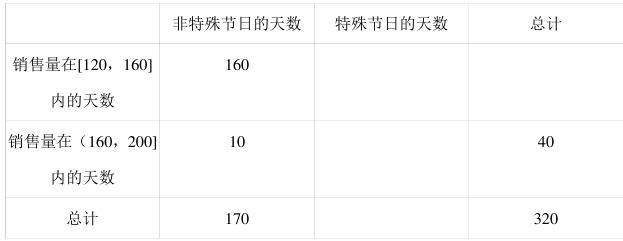
（1） 填写上表， 判断是否有 99%的把握认为“每天的玫瑰花的销售量与特殊节日有关”？

（2） 若按分层抽样的方式， 从上述表格的特殊节日中抽取 5 天作为一个样本， 再从这个样本中抽取 2 天加以分析研究， 求这两天玫瑰花的销售量在[120， 160]内的概率．

image.png

标记 纠错
18.

已知数列{a n }的各项均为正数， 记 S n 为{a n }的前 n 项和， 从下面①②③中选取两个作为条件， 证明另外一个成立

image.png

标记 纠错
19.

已知直三棱柱 ABC﹣ A 1 B 1 C 1 中， 侧面 AA 1 B 1 B 为正方形， AB＝BC＝2， E， F分别为 AC 和 CC 1 的中点， D 为棱 A 1 B 1 上的点， BF⊥A 1 B 1 ．

（1） 证明： BF⊥DE；

（2） 当 B 1 D 为何值时， 面 BB 1 C 1 C 与面 DFE 所成的二面角的正弦值最小？

image.png

标记 纠错
20.

抛物线 C 的顶点为坐标原点 O， 焦点在 x 轴上， 直线 l： x＝1 交 C 于 P， Q 两点， 且 OP⊥OQ． 已知点 M（2， 0）， 且⊙M与 l 相切．

（1） 求 C， ⊙M的方程；

（2） 设 A 1 ， A 2 ， A 3 是 C 上的三个点， 直线 A 1 A 2 ， A 1 A 3 均与⊙M 相切． 判断直线 A 2 A 3与⊙M的位置关系， 并说明理由．

标记 纠错
21.

image.png

（1） 当 a＝2 时， 求 f（x） 的单调区间；

（2） 若曲线 y＝f（x） 与直线 y＝1 有且仅有两个交点， 求 a 的取值范围

标记 纠错
22.

在直角坐标系 xOy 中， 以坐标原点为极点， x 轴正半轴为极轴建立极坐标系，曲线 C 的极坐标方程为 ρ＝2√2cosθ．

（1） 将 C 的极坐标方程化为直角坐标方程；

image.png

标记 纠错
23.

image.png

标记 纠错

答题卡（剩余 道题）

单选题
1 2 3 4 5 6 7 8 9 10 11 12
填空题
13 14 15 16
问答题
17 18 19 20 21 22 23
00:00:00
暂停
交卷
友情链接

答案圈武汉生活网吾爱诗经网

Copyright © 2018-2022 http://tk.mxqe.com/ Corporation, All Right Reserved 客服联系：2645034912@qq.com  备案号：鄂ICP备17009702号-1