当前位置：首页 → 学历类 → 高考 → 数学（理科）->2022年吉林省高考理科数学押题试卷

2022年吉林省高考理科数学押题试卷

卷面总分：23分 答题时间：240分钟 试卷题量：23题 练习次数：105次
单选题 （共12题，共12分）
1.

已知复数 z 在复平面内对应的点的坐标为（2， ﹣ 1）， 则|z﹣ i|＝（）

  • A. √2
  • B. 2
  • C. 2√2
  • D. 8
标记 纠错
2.

image.png

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
3.

image.png

  • A. {0， 2， 4}
  • B. {0， 1， 4}
  • C. {0， 1}
  • D. {0， 4}
标记 纠错
4.

我国冰雪健儿自 1992 年实现冬奥奖牌数 0 的突破， 到北京冬奥会结束， 共获得 77 块奖牌． 现将 1992 年以米我国冬奥会获得奖牌数量统计如表：

image.png

则 1992 年以来我国获得奖牌数的中位数为（）

  • A. 8
  • B. 9
  • C. 10
  • D. 11
标记 纠错
5.

 下列函数是偶函数， 且在区间（﹣ ∞， 0） 上为增函数的是（）

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
6.

在某次展会中， 有来自北京、 上海、 长春和杭州的四名志愿者， 现将这四名志愿者分配到这四个城市的代表团服务， 每个代表团只分配到其中一名志愿者， 则这四名志愿者中恰有两名为自己家乡代表团服务的概率为（）

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
7.

image.png

  • A. 4
  • B. 8
  • C. 12
  • D. 16
标记 纠错
8.

已知 f （x） ＝ax+a+cosx（a∈R）， 则在曲线 y＝f （x） 上一点（0， 2） 处的切线方程为（）

  • A. x﹣ y+2＝0
  • B. x+y﹣ 2＝0
  • C. 2x﹣ y+2＝0
  • D. 2x+y﹣ 2＝0
标记 纠错
9.

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
10.

某同学在学校组织的通用技术实践课上制作了一件工艺品， 该工艺品可以看成是一个球被一个棱长为 4 的正方体的六个面所截后中间剩余部分（球心与正方体中心重合）， 若其中一个截面圆的周长为 2π， 则该球的表面积为（）

  • A. 20π
  • B. 16π
  • C. 12π
  • D. 8π
标记 纠错
11.

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
12.

image.png

  • A. a＞b＞c
  • B. b＞a＞c
  • C. c＞a＞b
  • D. b＞c＞a
标记 纠错
填空题 （共4题，共4分）
13.

image.png

标记 纠错
14.

image.png

标记 纠错
15.

image.png

标记 纠错
16.

image.png

标记 纠错
问答题 （共7题，共7分）
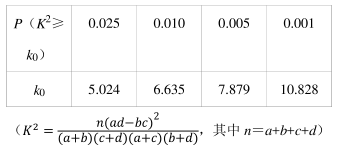
17.

从某地区高中二年级学生中随机抽取质量监测数学得分在 120 分以下和 120 分以上（含 120 分） 的学生各 250 名作为样本（全体高二学生均参加监测）， 分别测出他们的注意力集中水平得分， 统计如表．

image.png

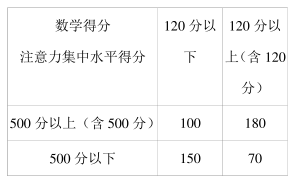
（1） 若将学生在质量监测中数学得分在 120 分以上（含 120 分）． 定义为数学成绩优秀，将学生注意力集中水平得分在 500 分以上（含 500 分） 称为注意力集中水平高； 试问：能否有 99%以上的把握认为数学成绩优秀与注意力集中水平高有关？

（2） 若将上述样本的频率视为概率， 现从该地区所有高二学生中随机抽取 100 人， 设抽取到的数学得分在 120 分以上（含 120 分） 且注意力集中水平得分在 500 分以上（含 500分） 的人数为随机变量 X， 求 X的数学期望．

image.png

标记 纠错
18.

image.png

image.png

标记 纠错
19.

直三棱柱 ABC﹣ A 1 B 1 C 1 中， AA 1 B 1 B 为正方形， AB＝BC， ∠ABC＝120° ， M为棱 BB 1 上任意一点， 点 D、 E 分别为 AC、 CM的中点．

（1） 求证： DE∥平面 AA 1 B 1 B；

（2） 当点 M为 BB 1 中点时， 求直线 B 1 C 和平面 CDM所成角的正弦值．

image.png

标记 纠错
20.

image.png

image.png

标记 纠错
21.

已知圆 M过点（1， 0）， 且与直线 x＝﹣ 1 相切．

（1） 求圆心 M的轨迹 C 的方程；

（2） 过点 P（2， 0） 作直线 l 交轨迹 C 于 A、 B 两点， 点 A 关于 x 轴的对称点为 A′ ，过点 P 作 PQ⊥A′ B， 垂足为 Q， 在平面内是否存在定点 E， 使得|EQ|为定值． 若存在，求出点 E 的坐标； 若不存在， 请说明理由．

标记 纠错
22.

image.png

image.png

标记 纠错
23.

设函数 f（x） ＝|x+1|， g（x） ＝|2x﹣ 1|．

（1） 解关于 x 的不等式 f（x） ﹣ g（x） ＞1；

（2） 若 2f（x） +g（x） ＞ax+2， 求实数 a 的取值范围．

标记 纠错

答题卡（剩余 道题）

单选题
1 2 3 4 5 6 7 8 9 10 11 12
填空题
13 14 15 16
问答题
17 18 19 20 21 22 23
00:00:00
暂停
交卷
友情链接

答案圈武汉生活网吾爱诗经网

Copyright © 2018-2022 http://tk.mxqe.com/ Corporation, All Right Reserved 客服联系：2645034912@qq.com  备案号：鄂ICP备17009702号-1