6.在一块电路板的上下两端分别有n个接线柱。根据电路设计,用(i,π(i))表示将上端接线柱i与下端接线柱π(i)相连,称其为该电路板上的第i条连线。如图4-1所示的π(i)排列为{8,7,4,2,5,1,9,3,10,6}。对于任何1≤i<j≤n,第i条连线和第j条连线相交的充要条件是π(i)>π(j)。
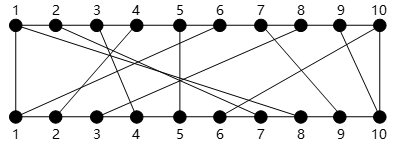
图4-1电路布线示意
在制作电路板时,要求将这n条连线分布到若干绝缘层上,在同一层上的连线不相交。现在要确定将哪些连线安排在一层上,使得该层上有尽可能多的连线,即确定连线集Nets={(i,π(i)),1≤i≤n}的最大不相交子集。
【分析问题】
记N(i,j)={t|(t,π(t))∈Nets,t≤i,π(t)≤j}。N(i,j)的最大不相交子集为MNS(i,j),size(i,j)=|MNS(i,j)|。
经分析,该问题具有最优子结构性质。对规模为n的电路布线问题,可以构造如下递归式:

【C代码】
下面是算法的C语言实现。
(1)变量说明
size[i][j]:上下端分别有i个和j个接线柱的电路板的第一层最大不相交连接数
pi[i]:π(i),下标从1开始
(2)C程序
#include"stdlib.h"
#include<stdio.h>
#define?N?10/*问题规模*/
int m=0;/*记录最大连接集合中的接线柱*/
void maxNum(int pi[],int size[N+1][N+1],int n){/*求最大不相交连接数*/
int i,j;
for(j=0;j<pi[1];j++)size[1][j]=0;/*当j<π(1)时*/
for(j=pi[1];j<=n;j++)(1);/*当j>=π(1)时*/
for(i=2;i<n;i++){
for(j=0;j<pi[i];j++)(2);/*当j<pi[i]时*/
for(j=pi[i];j<=n;j++){/*当j>=c[i]时,考虑两种情况*/
size[i][j]=size[i-1][j]>=size[i-1][pi[i]-1]+1?size[i-1][j]:size[i-1][pi[i]-1]+1;
}
}
/*最大连接数*/
size[n][n]=size[n-1][n]>=size[n-1][pi[n]-1]+1?size[n-1][n]:size[n-1][pi[n]-1]+1;
}
/*构造最大不相交连接集合,net[i]表示最大不相交子集中第i条连线的上端接线柱的序号*/
void constructSet(int pi[],int size[N+1][N+1],int n,int net[n]){
int i,j=n;
m=0;
for(i=n;i>1;i--){/*从后往前*/
if(size[i][j]!=size[i-1][j]){/*(i,pi[i])是最大不相交子集的一条连线*/
(3);/*将i记录到数组net中,连接线数自增1*/
j=pi[i]-1;/*更新扩展连线柱区间*/
}
}
if(j>=pi[1])net[m++]=1;/*当i=1时*/
}
【问题1】(6分)
根据以上说明和C代码,填充C代码中的空(1)~(3)。
【问题2】(6分)
据题干说明和以上C代码,算法采用了(4)算法设计策略。
函数maxNum和constructSet的时间复杂度分别为(5)和(6)(用O表示)。
【问题3】(3分)
若连接排列为{8,7,4,2,5,1,9,3,10,6},即如图4-1所示,则最大不相交连接数为(7),包含的连线为(8)(用(i,π(i))的形式给出)。