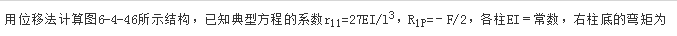设某种商品的每周的需求量X是服从区间［10，30］上均匀分布的随机变量，而经销商店进货数量为区间［10，30］中的某一整数，商店每销售一单位商品可获利500元，若供大于求则削价处理，每处理1单位商品亏损100元，若供不应求，则可从外部调剂供应，此时每个单位商品仅获利300元，为使商店所获利润期望值不少于9280元，试确定最少进货量.

查看答案 纠错

答案：

本题解析：

【简解】本题是一个利用均匀分布，随机变量的数学期望的应用题.关键是求出利润的函数g(X；a)，其中a是进货量.

当X>a时，进货全售出，得利润500a，再去调剂获利300(X-a)

当X≤a时，销售得利500X，多余的削价处理亏损100(a-X)

所以g(X；a)=

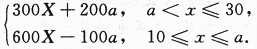
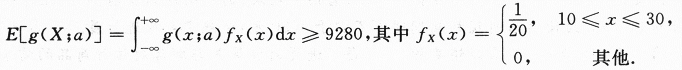
解得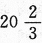≤a≤26，最小进货量为21单位，

更新时间：2021-10-10 20:24

你可能感兴趣的试题

单选题

• A.1∶1
• B.1∶（-1）
• C.1∶2
• D.1∶（-2）

查看答案

单选题

• A.见图A
• B.见图B
• C.见图C
• D.见图D

查看答案

单选题

• A.见图A
• B.见图B
• C.见图C
• D.见图D

查看答案

单选题

• A.0.65cm
• B.4.02cm
• C.0.223cm
• D.0.472cm

查看答案

单选题

• A.见图A
• B.见图B
• C.见图C
• D.见图D

查看答案

单选题

• A.0.273；－48
• B.0.273；48
• C.0.294；－48
• D.0.294；48

查看答案

单选题

• A.0.500；+5.0kN·m
• B.0.571；+10.0kN·m
• C.0.625；+10.0kN·m
• D.0.667；+5.0kN·m

查看答案

单选题

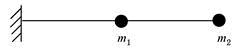
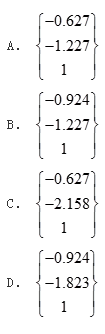
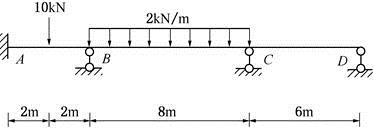
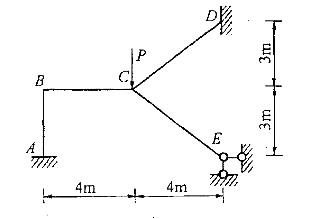
图示结构，各杆EI=常数，不计轴向变形，MBA及MCD的状况为:

• A.MBA≠0，MCD=0
• B.MBA=0，MCD≠0
• C.MBA=0，MCD=0
• D.MBA≠0，MCD≠0

查看答案

单选题

• A.－Fl/8
• B.－Fl/9
• C.Fl/8
• D.Fl/9

查看答案

单选题

• A.-12
• B.-6
• C.5
• D.8

查看答案