当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->在“平行线的性质”的新授课上,一位教师设计了如下的教学片段:
在“平行线的性质”的新授课上,一位教师设计了如下的教学片段:一、复习
1.如何用同位角、内错角、同旁内角来判定两条直线是否平行?
2.把它们已知和结论颠倒一下,可得到怎样的语句?"它们正确吗?二、新授
1.实验观察.发现平行线第一个性质。
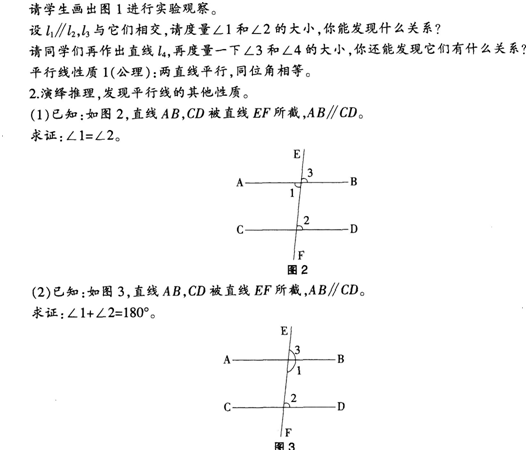
在此基础上指出:“平行线的性质2(定理)”和“平行线的性质3(定理)”。3.平行线判定与性质的区别与联系。
投影:将判定与性质各三条全部打出。
? ? (1)性质:根据两条直线平行,去证角的相等或互补。(2)判定:根据两角相等或互补,去证两条直线平行。联系是:它们的条件和结论是互逆的。性质与判定要证明的问题是不同的。
? ? 针对上述材料,完成下列任务。
? ? (1)本教学片段运用什么导入方法?并简述这种导入方法的优点。(7分)
? ?(2)简述本节课内容的教学目标。(5分)
? ? (3)本节课的重点和难点分别是什么?(5分)
? ? (4)为了进一步巩固平行线的性质定理,请设计相应例题和习题各一个,并写明解题思路。(13分)
(1)本教学片段运用了复习导人。这种导入方法利用新旧知识间的逻辑联系,即旧知识是新知识的基础,新知识是旧知识的发展与延伸,从而找出新旧知识联结的交点,由旧知识的复习迁移到新知识的学习上来导入新课。通过这种方法导入新课可以淡化学生对新知识的陌生感,使学生迅速将新知识纳入原有的知识结构中,能有效降低学生对新知识的认知难度。 (2)①理解平行线的性质和判定的区别:
②掌握平行线的三个性质,并能运用它们作简单的推理。(3)重点:平行线的三个性质。
难点:平行线的三个性质和怎样区分性质定理和判定定理。
(4)例题:如图所示,已知:AD//BC,∠AEF=∠B,求证:AD//EF。
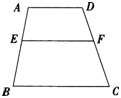
分析:(执果索因)从图直观分析,欲证AD//只需∠A+∠EF=1800
(由因求果)因为AD//BC,所以∠A+∠B=1800,又∠B=∠AEF,所以∠A+∠AEF=180。成立。于是得证。
证明:因为AD//BC.
所以∠A+∠B=1800。(两直线平行,同旁内角互补)因为£AE聘[曰,(已知)
所以∠A+∠AEF=1800,(等量代换)
所以AD//EF.(同旁内角互补,两条直线平行)
练习:如图所示,已知:AE平分∠BAC,C E ,且AB//CD。且AB∥CD
求证:∠l+∠2=900。
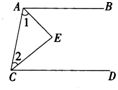
证明:因为AB//CD.
所以∠BAC+∠ACD=1800.
又因为AE平分∠BAC,CE平分∠ACD,
教学过稈具冇哪些基木特点?
简述开展好课外活动的基木要求。
开展好课外活动的基木要求:
简要冋答少年儿童的身心发展的个別差异性。
班主任要统一各方而的___________ ,同家庭与社会密切配合。
小学德育的基木途径是______________ 。
课的类型大致可分为________ 和_________ 两大类。
学生是生活在一定的社会关系中,具冇特定的_________的人。
师生在人格上是_________ 的关系。
德育的个体功能可以描述为德育对个体生存、发展、________ 发生影响的三个方而。
教学工作的基木环节包括_______ 、______、______、_______和______五个方而。