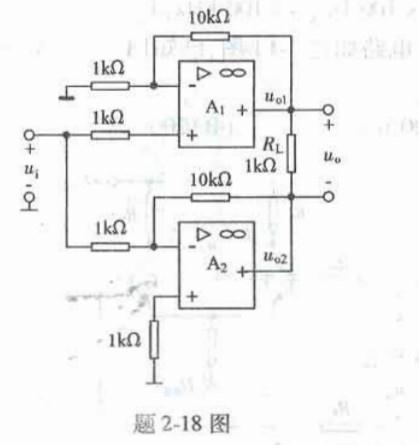
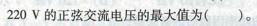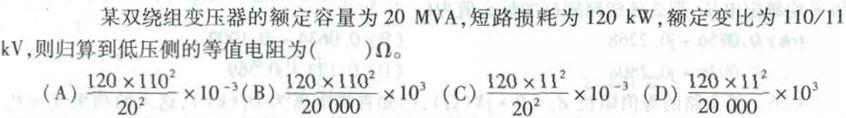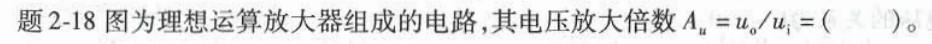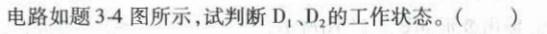对于函数f(x,y)=xy,原点(0,0)( )。
驻点是指函数f(x,y)一阶偏导数均等于零的点。对于函数f(x,y)=xy,fx=y,fy=x,则fx(0,0)=fy(0,0)=0。因此,原点(0,0)是函数的驻点。
设函数f(x,y)在点P0(x0,y0)的某个邻域内具有二阶连续偏导数,且P0(x0,y0)是驻点。设A=fxx(x0,y0),B=fxy(x0,y0),C=fyy(x0,y0),则:
①当B2-AC<0时,点P0(x0,y0)是极值点,且当A<0时,点P0(x0,y0)是极大值;当A>0时,点P0(x0,y0)是极小值点;
②当B2-AC>0时,点P0(x0,y0)不是极值点;
③当B2-AC=0时,点P0(x0,y0)有可能是极值点也有可能不是极值点。
对于函数f(x,y)=xy,A=fxx(x0,y0)=0,B=fxy(x0,y0)=1,C=fyy(x0,y0)=0,则B2-AC=1>0。因此,原点(0,0)不是极值点。
综上,原点(0,0)是驻点但非极值点。