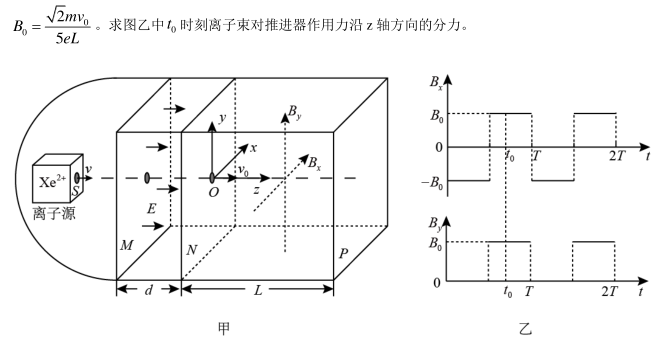
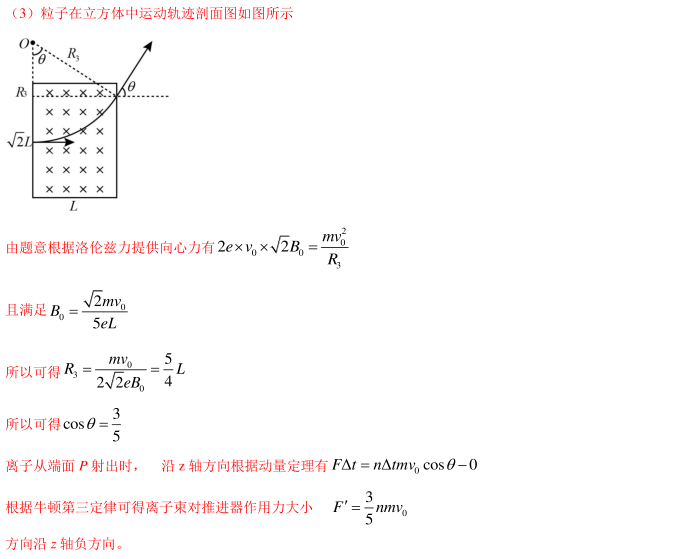
如图甲所示,空间站上某种离子推进器由离子源、间距为d的中间有小孔的两平行金属板M、N和边长为L的立方体构成,其后端面Р为喷口。以金属板N的中心О为坐标原点,垂直立方体侧面和金属板建立x、y和z坐标轴。M、N板之间存在场强为E、方向沿z轴正方向的匀强电场;立方体内存在磁场,其磁感应强度沿z方向的分量始终为零,沿x和y方向的分量B和B,随时间周期性变化规律如图乙所示,图中B,可调。氩离子(Xe2+)束从离子源小孔S射出,沿z方向匀速运动到M板,经电场加速进入磁场区域,最后从端面Р射出,测得离子经电场加速后在金属板N中心点О处相对推进器的速度为v。已知单个离子的质量为m、电荷量为2e,忽略离子间的相互作用,且射出的离子总质量远小于推进器的质量。

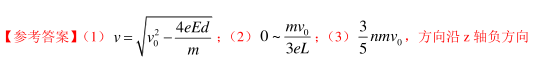

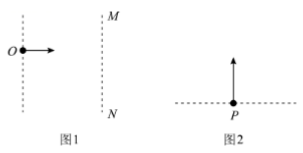
铯原子钟是精确的计时仪器。 图 1 中铯原子从 O 点以 100 m/s 的初速度在真空中做平抛运动, 到达竖直平面 MN 所用时间为t1; 图 2 中铯原子在真空中从 P 点做竖直上抛运动, 到达最高点 Q 再返回 P 点, 整个过程所用时间为t2。O点到竖直平面 MN 、 P 点到 Q 点的距离均为 0.2 m 。 重力加速度取g=10m/s2, 则t1:t2为()
“祝融号” 火星车登陆火星之前, “天问一号” 探测器沿椭圆形的停泊轨道绕火星飞行, 其周期为 2 个火星日, 假设某飞船沿圆轨道绕火星飞行, 其周期也为 2 个火星日。 已知一个火星日的时长约为一个地球日, 火星质量约为地球质量的 0.1 倍, 则该飞船的轨道半径与地球同步卫星的轨道半径的比值约为( )

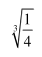
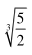
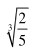
如图,距离为 d的两平行金属板 P、Q 之间有一匀强磁场, 磁感应强度大小为B1,一束速度大小为 v 的等离子体垂直于磁场喷入板间。相距为 L 的两光滑平行金属导轨固定在与导轨平面垂直的匀强磁场中, 磁感应强度大小为B2, 导轨平面与水平面夹角为θ, 两导轨分别与 P、 Q 相连。 质量为m、电阻为 R 的金属棒 ab 垂直导轨放置, 恰好静止。 重力加速度为 g, 不计导轨电阻、 板间电阻和等离子体中的粒子重力。 下列说法正确的是( )
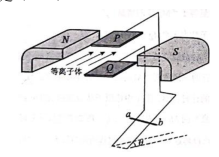




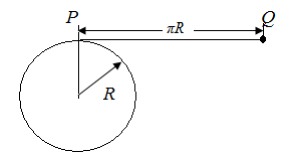
一半径为 R 的圆柱体水平固定,横截面如图所示, 长度为πR、 不可伸长的轻细绳, 一端固定在圆柱体最高点 P 处, 另一端系一个小球。 小球位于 P 点右侧同一水平高度的 Q 点时, 绳刚好拉直。 将小球从 Q 点由静止释放, 当与圆柱体未接触部分的细绳竖直时, 小球的速度大小为(重力加速度为 g, 不计空气阻力)( )
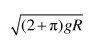
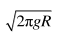
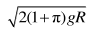
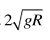
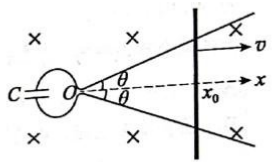
如图,两光滑导轨水平放置在竖直向下的匀强磁场中, 磁感应强度大小为 B。导轨间距最窄处为一狭缝, 取狭缝所在处 O 点为坐标原点。 狭缝右侧两导轨与 x 轴夹角均为θ, 一电容为 C的电容器与导轨左端相连。 导轨上的金属棒与 x 轴垂直, 在外力 F 作用下从 O 点开始以速度 v 向右匀速运动, 忽略所有电阻。 下列说法正确的是( )
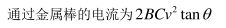
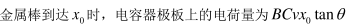
如图,发电机的矩形线圈长为2L、宽为L、匝数为N、放置在磁感应强度大小为B 的匀强磁场中,理想变压器的原、副线圈匝数分别为n0、n1、n2两个副线圈分别接有电阻R1和R2。当发电机线圈以角速度ω匀速转动时, 理想电流表读数为 I。不计线圈电阻,下列说法正确的是( )
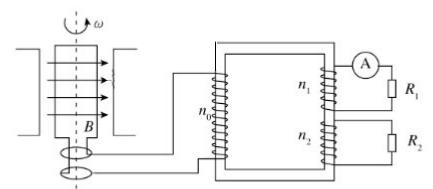
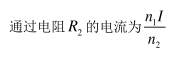


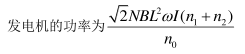
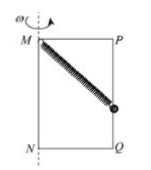
如图,矩形金属框 MNQP 竖直放置, 其中 MN 、 PQ 足够长, 且 PQ 杆光滑。一根轻弹簧一端固定在 M点, 另一端连接一个质量为 m 的小球, 小球穿过 PQ 杆。 金属框绕 MN 轴分别以角速度ω和ω'匀速转动时, 小球均相对 PQ 杆静止。若ω'>ω,则与以ω匀速转动时相比, 以ω'匀速转动时( )
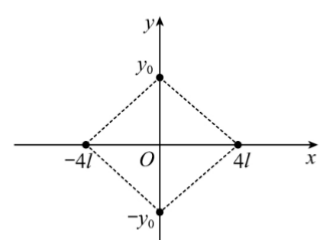
如图,四个电荷量均为q(q >0)的点电荷分别放置于菱形的四个顶点,其坐标分别为(4l,0)、(-4l,0)、(0,y0)和(0,-y0),其中x轴上的两个点电荷位置固定,y轴上的两个点电荷可沿y轴对称移动(y≠0)。下列说法正确的是()
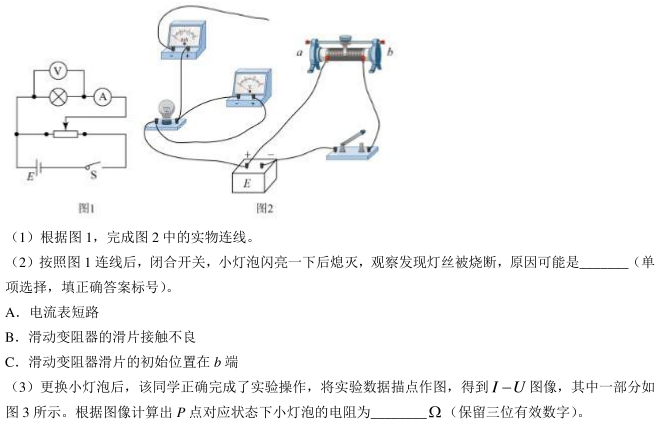
某同学研究小灯泡的伏安特性,实验室提供的器材有: 小灯泡(6.3 V,0.15 A),直流电源(9 V),滑动变阻器, 量程合适的电压表和电流表, 开关和导线若干。 设计的电路如图 1 所示。
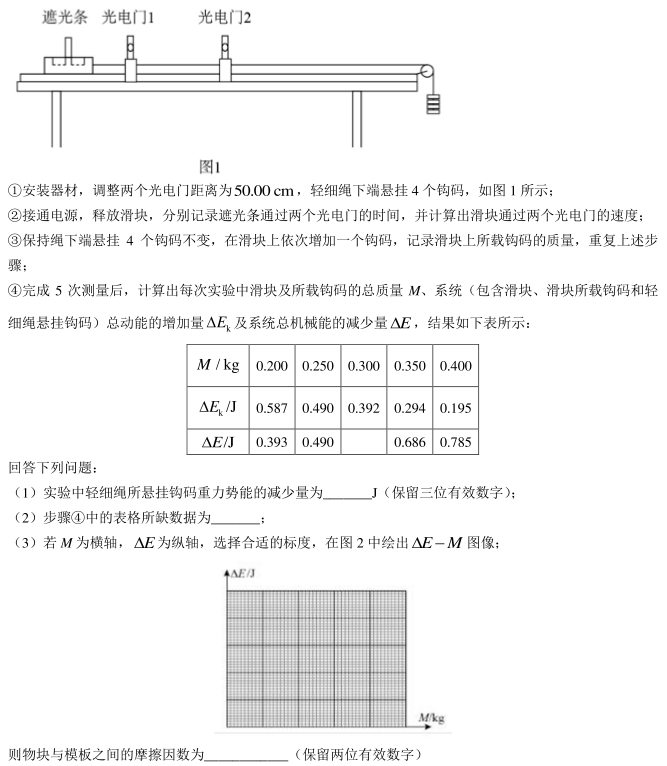
某同学利用图 1 中的实验装置探究机械能变化量与力做功的关系。所用器材有: 一端带滑轮的长木板、 轻细绳、 50 g 的钩码若干、 光电门 2 个、 数字计时器、 带遮光条的滑块(质量为 200 g , 其上可放钩码)、 刻度尺。 当地重力加速度为9.80m/s2,实验操作步骤如下: