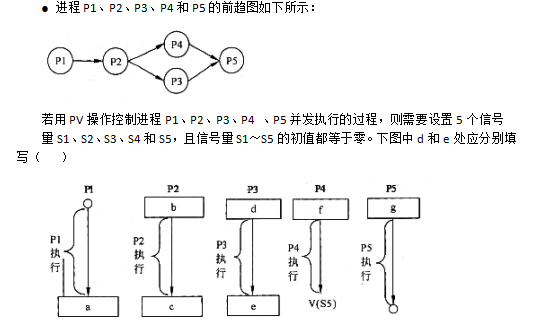
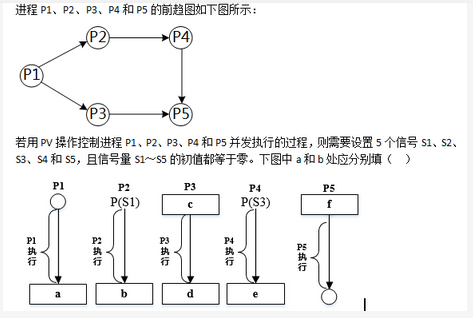
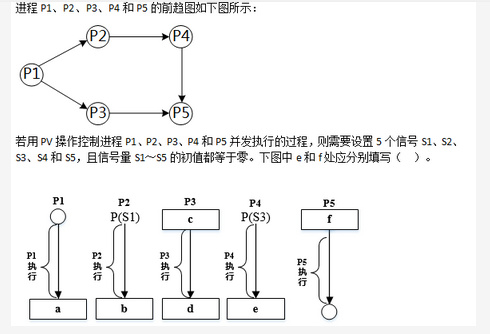
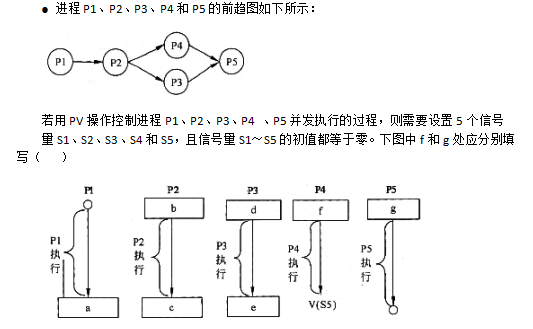
RSA是一种公开密钥加密算法。其原理是:已知素数p、q,计算n=pq,选取加密密钥e,使e与(p-1)×(q-1)互质,计算解密密钥d ≡ e-1 mod((p-1)×(q-1))。其中n、e是公开的。如果M、C分别是明文和加密后的密文,则加密的过程可表示为( )。
假定Exy(M)表示利用X的密钥Y对消息M进行加密,Dxy(M)表示利用X的密钥Y对消息 M 进行解密,其中 Y=P 表示公钥,Y=S 表示私钥。A 利用 RSA 进行数字签名的过程可以表示为( ),A 利用RSA 实施数字签名后不能抵赖的原因是( )。
问题1选项
答案: A、B、C。
本题考查RSA的基本知识。
RSA的原理如题所述,加密过程是先将明文分成多个组,每组看成一个整数M,加密就是计算C=Memod n。
RSA可以用于数字签名,其过程是:用签名者的私钥对消息加密,然后再用接收者的公钥对加密后的内容加密。因为签名过程中用签名者的私钥对消息进行了加密,且只有签名者本人知道其私钥,因此这样的签名是不能抵赖的。