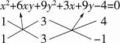
方程x2+6xy+my2+3x+ny-4=0表示的图形是两条互相垂直的直线。
（1）m=5，n=-1；
（2）m=9，n=9。
①条件（1）：根据条件得x2+6xy+5y2+3x-y-4=0，
由双十字相乘得（x+5y+4）（x+y-1）=0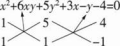
x+5y+4=0或x+y-1=0，
图形为两条直线，A1A2+B1B2=1×1+5x1=6≠0，故两直线相交不垂直，所以条件（1）不充分。
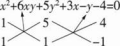
②条件（2）：根据条件得x2+6xy+9y2+3x+9y-4=0，由双十字相乘得（x+3y+4）（x+3y-1）=x+3y+4=0或x+3y-1=0，图形为两条斜率相同的直线，故两直线平行，所以条件（2）不充分。
③（1）+（2）：两条件矛盾，无法联合，条件（1）和（2）联合不充分。
