阅读以下说明和流程图,填补流程图中空缺,将解答填入答题纸对应栏内。
[说明]
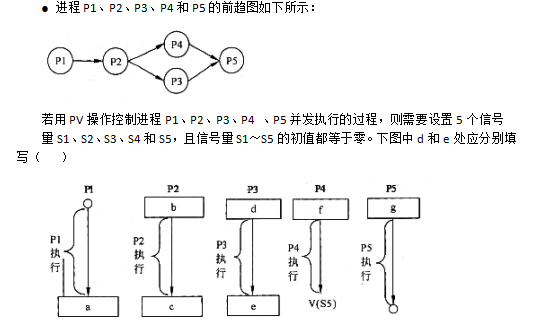
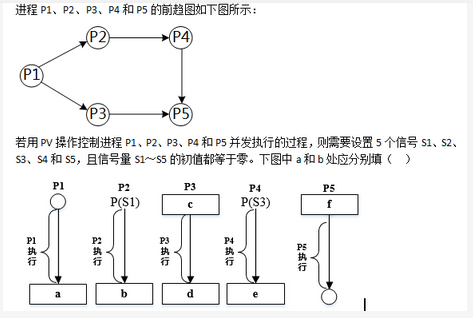
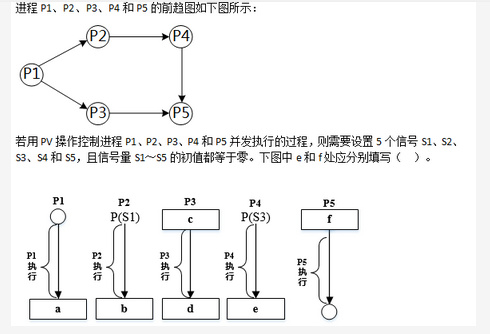
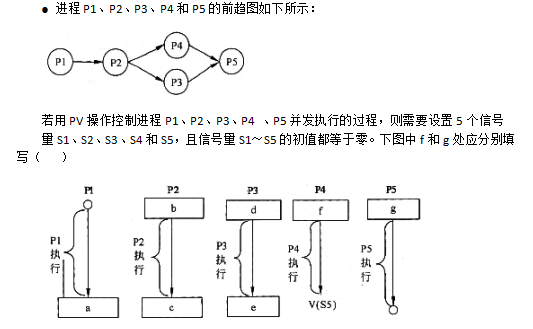
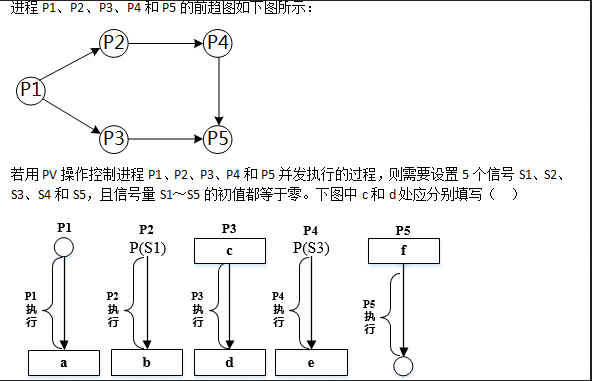
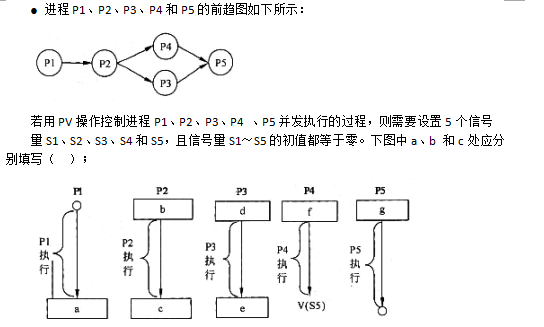
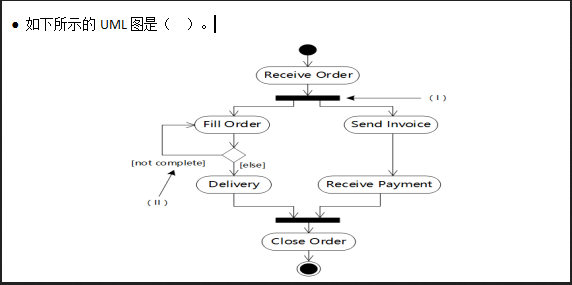
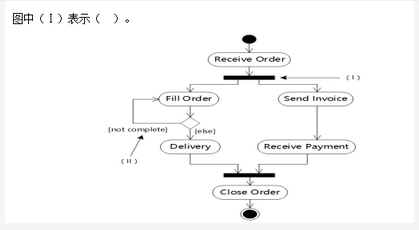
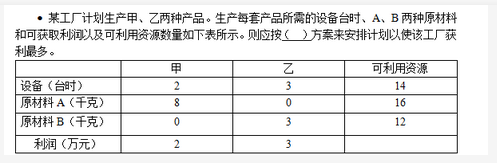
下面流程图功能是:在给定一个整数序列中查找最长连续递增子序列。设序列存放在数组A[1:n](n≥2)中,要求寻找最长递增子序列A[K:K+L-1](即A[K]<A[K+1]<…<A[K+L-1])。流程图中,用Kj和Lj分别表示动态子序列起始下标和长度,最后输出最长递增子序列起始下标K和长度L。
例如,对于序列A={1,2,4,4,5,6,8,9,4,5,8},将输出K=4,L=5。
[流程图]
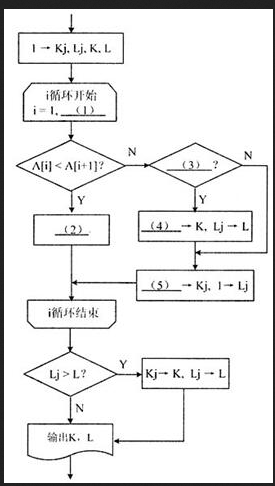
注:循环开始框内应给出循环控制变量初值和终值,默认递增值为1,格式为:循环控制变量=初值,终值
n-1
Lj+1→Lj
Lj>L
Kj
i+1
【解析】
本题考查程序员在设计算法,理解并绘制程序流程图方面能力。
本题目标是:在给定一个整数序列中查找最长连续递增子序列。查找方法是:对序列中数,从头开始逐个与后面邻接数进行比较。若发现后面数大于前面数,则就是连续递增情况;若发现后面数并不大,则以前查看数中,要么没有连续递增情况,要么连续递增情况已经结束,需要再开始新查找。
为了记录多次可能出现连续递增情况,需要动态记录各次出现递增子序列起始位置(数组下标K1)和长度(Lj)。为了求出最大长度递增子序列,就需要设置变量L和K,保存迄今为止最大Lj及其相应Kj。正如打擂台一样,初始时设置擂主L=1,以后当Li>L时,就将Lj放到L中,作为新擂主。擂台上始终是迄今为止连续递增序列最大长度。而Kj则随Lj→L而保存到K中。
由于流程图中最关键步骤是比较A[i]与A[i+1],因此对i循环应从1到n-1,而不是1到n。最后一次比较应是"A[n-1]<A[n]?"。因此(1)处应填n-1。
当A[i]<A[i+1]成立时,这是递增情况。此时应将动态连续递增序列长度增1,因此(2)处应填写Li+1→Lj。
当A[i]<A[i+1]不成立时,表示以前可能存在连续递增已经结束。此时动态长度Li应与擂台上长度L进行比较。即(3)处应填Lj>L。
当Lj>L时,则Lj将做新擂主(Lj→L),同时执行Kj→K。所以(4)处应填Kj。
当Lj→L不成立时,L不变,接着要从新下标i+1处开始再重新查找连续递增子序列。因此(5)处应填i+1。长度Lj也要回到初始状态1。
循环结束时,可能还存在最后一个动态连续子序列(从下标Kj那里开始有长度Lj子序列)没有得到处理。因此还需要再打一次擂台,看是否超过了以前擂主长度。一旦超过,还应将其作为擂主,作为查找结果。