当前位置：首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->在学习了“集合的基本运算”后，教师要求学生解决如下问题。设A
在学习了“集合的基本运算”后，教师要求学生解决如下问题。
设A={x|x2-x-6=0}，B={x|2ax+1=0}，若A∩B=B，求符合条件的。有多少个?
一位学生给出的解法如下：集合A={-2，3}，由A∩B=B可知，B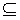
A，当方程2ax+1=0的解为-2或3时，代入得
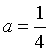或
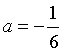。所以符合条件的a有2个。
问题：
（1）请指出该解法的错误之处，分析错误原因，并给出正确解法；
（2）针对该题的教学，谈谈该如何设置问题，帮助学生避免出现上述错误。
（1）该学生忽略了空集是任何集合的子集。可能造成这种错误的原因有以下几点：
①该学生对集合的性质掌握不够透彻；
②该学生对分类讨论思想的运用不够熟练；
③该学生没有注意空集是任何集合的子集这一重要性质。
正确解法如下：
集合A={-2，3}，由A∩B=B知B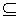
A，当B=?时，即方程2ax+1=0无解，此时a=0；当B≠?时，即方程2ax+1=0的解为-2或3时，代入得a=
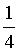或a=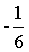
。所以符合条件的a有3个。
（2）针对本题，结合案例中学生m现的错误，教师应该根据该题的教学步骤，在教学过程中，采取相应的策略设置问题。下面结合教学过程进行分析：
①教师与学生一起回忆旧知，提出问题“集合的相关性质有哪些”。
②教师通过提问引导学生复习空集及其性质。
③教师结合本题引导学生根据集合的性质，运用分类讨论思想解题，将集合B是空集的情况优先进行讨论。
《义务教育数学课程标准（2011年版）》强调，课程内容要反映社会的需要、数学的特点，要符合学生的认知规律。课程内容的组织要重视过程，处理好（）的关系。
设α是某一方程组的解向量，k为某一常数，则kα也为该方程组的解向量。（ ）
案例：
在有理数运算的课堂教学片段中，某学生的板演如下：
针对该学生的解答，教师进行了如下教学：
师：请仔细检查你的演算过程，看是否正确无误？
生：好像正确吧。
请分析例题1、例题2中每一步运算的依据。（10分）
初中数学课程是一门国家课程，其主要内容包括课程目标、教学内容、教学过程和( )等
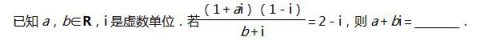
教学工作的中心环节是（ ）。
教师职业道德区别于其他职业道德的显著标志就是（ ）。
教育的本体功能之一是( )。
