当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->“两角差的余弦公式”是高中数学教材中的重要公式,只有对两角差
“两角差的余弦公式”是高中数学教材中的重要公式,只有对两角差的余弦有了认识,才能够以此为基础推导其他三角恒等变换公式。这是一个逻辑推理过程,也是一个认识三角函数式的特征,体会三角恒等变换特点的过程。
请完成下列问题:
(1)设计“两角差的余弦公式”的教学目标;
(2)写出“两角差的余弦公式”的教学重点和难点;
(3)-写出“两角差的余弦公式”的探究过程(要求使学生意识到,向量方法可能是解决问题的工具)。
(1)教学目标
知识与技能目标:
①通过对两角差的余弦公式的推导,了解应用向量解决数学问题的方法;
②通过公式的灵活应用,掌握两角差的余弦公式。
过程与方法目标:
①通过两角差的余弦公式的推导过程,体会向量在代数、几何方面运用的方式方法;
②培养分类讨论思想、转化和化归思想、数形结合思想。
情感态度与价值观目标:
通过引导学生主动参与、大胆猜想、独立探索,激发学习兴趣,形成探究、证明、应用的获取知识的方式;从应用中体会数学的严谨,形成理性思维,体会向量及两角差的余弦公式的运用价值。
(2)教学重难点
重点:两角差的余弦公式的运用。
难点:用两角差的余弦公式进行简化、计算及逆用公式等。
(3)教学探究过程
一、问题引入
问题l.我们已经知道了
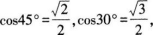
由此我们能得到cos15°的值吗?
问题2.对于cos(α-β)=cosα-cosβ,你们同意这个观点吗?说说理由。
二、探索新知
活动1
(教师活动)提出问题:究竟该如何计算cos(α-β)?对于求角的余弦这种问题,我们有哪些方法?
(学生活动)回忆三角函数定义、三角函数线以及平面向量数量积运算等相关知识。
活动2
(教师活动)引导学生尝试用向量的方法来探究如何计算cos(α-β)。
先复习两个向量数量积的定义与坐标运算公式,定义式:a·b=|a|·|b|·cosθ;坐标式:a·b=x1x2+y1y2。
(学生活动)在平面直角坐标系中作单位圆,以x轴非负半轴为始边作角α,β,它们的终边与单位圆O的交点分别为A,B,则A(cosα/,sinα),B(cosβ,sinβ)。试用A,B两点的坐标表示∠AOB的余弦值。
(教师活动)引导学生经历用向量方法探究,求cos(α-β),结合图形,明确应选择哪几个向量,它们怎么用坐标表示,怎样利用数量积计算公式得到推导结果。
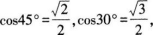
活动3
(教师活动)引导学生思考α,β,α-β的范围,完善公式的推导。
(学生活动)提出α-β的任意性,而向量夹角为[0,π],学生产生疑惑:α-β与向量之间的夹角θ有什么关系呢?
(教师活动)几何画板动态展示,引导学生结合计算机图形语言和三角函数诱导公式对公式的严密性进行论证。
①α-β∈[0,n],α-β=θ+2kn;②α-β∈(n,2π],α-β=2kw-θ,根据终边相同的角的性质,有cos(α-β)=cosθ。
活动4
(教师活动)引导学生说出两角差的余弦公式的结构特点。
(学生活动)发现公式左边是差角的余弦,右边是单角同名三角函数值乘积之和。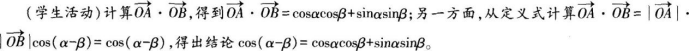
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )

案例:
在有理数运算的课堂教学片段中,某学生的板演如下:

针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。

请分析例题1、例题2中每一步运算的依据。(10分)
初中数学课程是一门国家课程,其主要内容包括课程目标、教学内容、教学过程和( )等
教师职业道德区别于其他职业道德的显著标志就是( )。
对高中数学的评价,下列说法错误的是( )。
