当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->针对“等差数列”的教学,某教师制定了如下教学目标。目标一:理
针对“等差数列”的教学,某教师制定了如下教学目标。
目标一:理解等差数列的概念,掌握等差数列的通项公式;
目标二:理解等差数列通项公式的推导方法,会运用等差数列的通项公式解决实际问题;
目标三:通过公式的推导过程,培养观察、分析、归纳能力和严密的逻辑思维能力。
(1)针对“等差数列”的内容,回答下列问题:
①分析学生已有的知识基础;
②设计一个等差数列的教学引人片段,并说明设计意图。
(2)请针对上述教学目标,完成下列任务:
①根据教学目标一、二,设计一个习题,帮助学生理解等差数列,并说明设计意图;
②根据教学目标二、三,设计推导等差数列通项公式的教学片段,并说明设计意图。
(1)①等差数列是高三年级所学习的必修5中的内容,此阶段的学生已经学习了函数的概念、性质和应用,对函数、方程思想的体会逐渐深刻,已经熟悉了由观察到抽象的数学教学过程,学生也学习了数列的概念与简单表示方法、通项公式、递推公式等概念。
此阶段学生的智力发展已经到了形式运演阶段,具备了较强的抽象思维能力和演绎推理能力;具备了一定的数学表达能力、数学分析能力和数据处理能力;具备学习等差数列所需的知识,但是在对一些等差数列的通项公式的求解过程中,学生尚欠缺基本的分析能力及处理经验。所以在教学过程中,教师要注重从具体生活实例出发,注重引导、启发以符合学生的心理发展特点,从而促进其思维能力进一步发展。
②引入环节
教师出示几个不同的数列:
1.0,5,10,l5,20,25;
2.一2,-1,0,1,2,3;
3.3,3,3,3,3,3;
4.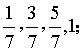
问题:请学生仔细观察以上数列,各个数列相邻两项之间有什么共同特征?
教师引导学生通过观察、类比、思考和交流得出结论。共同特征:从第二项起,每一项与它的前一项的差等于同一个常数。
教师根据学生给出的结论,为存在这种共同特征的数列起一个名字:等差数列。然后引出等差数列的定义。
【设计意图】给出几个不同的等差数列,让学生通过探索交流发现规律,从而提升学生分析问题的能力。
(2)①习题:已知等差数列8,5,2,…,
(1)请写出通项公式;
(2)请求出第20项的值;
(3)-16是这个数列中的第几项?
【设计意图】第一问目的是加深学生对等差数列中公差、通项公式的记忆,第二问是帮助学生理解通项公式的运用,第三问是公式的逆用,帮助学生进一步巩固等差数列的基础知识。
②教学片段
教师给出等差数列的定义,根据定义要求学生写出其中蕴含的递推公式,即an-an-1=d。
问题:能否根据等差数列定义得到的递推公式,推出数列的通项公式呢?
教师启发,引导学生可用首项和公差表示数列中的任意一项,学生分组探究,归纳总结通项公式。
预设:a2=a1+d.
a3=a2+d=a1+2d,
a4=a3+d=a1+3d,
猜想出:an=an-1+d=a1+(n-1)d。
问题:那么我们要如何证明此猜想成立呢?
教师启发引导学生根据递推公式an-an-1=d写出若干项,然后把等式左右两边都相加,得到递推公式,并介绍证明通项公式的方法为叠加法,即
a2-a==d,
a3-a2=d,
a4-a3=d,
……
an-1—an-2=d,
an-an-1=d,
两边叠加得到an-a1=(n-1)d,推出等差数列的通项公式an=a1+(n-1)d,当n=1时,通项公式也成立。
【设计意图】学生在引导下经由猜想归纳总结出等差数列的通项公式,学生的推理能力因此得到有效的锻炼。学生分组合作、自主探究可以培养学生解决问题的能力,增强其合作交流的意识。
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )

案例:
在有理数运算的课堂教学片段中,某学生的板演如下:

针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。

请分析例题1、例题2中每一步运算的依据。(10分)
初中数学课程是一门国家课程,其主要内容包括课程目标、教学内容、教学过程和( )等
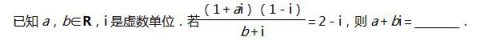
教师职业道德区别于其他职业道德的显著标志就是( )。
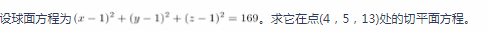
对高中数学的评价,下列说法错误的是( )。
