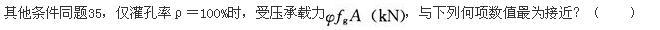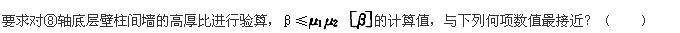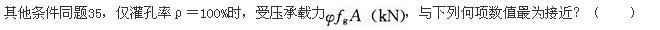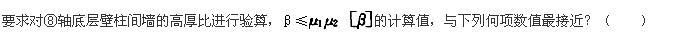某12层现浇框架结构,其中一榀中部框架的剖面如题图所示,现浇混凝土楼板,梁两侧无洞。底层各柱截面相同,2~12层各柱截面相同,各层梁截面均相同。梁、柱矩形截面线刚度ib0、ic0(单位:1010N·mm)注于构件旁侧。假定,梁考虑两侧楼板影响的刚度增大系数取《高层建筑混凝土结构技术规程》(JGJ 3—2010)中相应条文中最大值。
提示:①计算内力和位移时,采用D值法。
②D=α(12ic/h2),式中α是与梁柱刚度比有关的修正系数,对底层柱:α=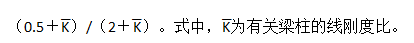
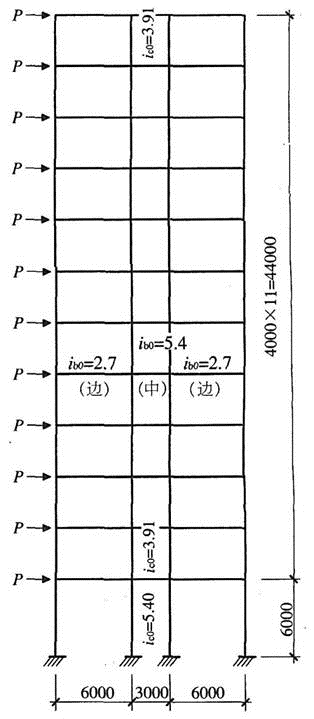
假定,该建筑物位于7度抗震设防区,调整构件截面后,经抗震计算,底层框架总侧移刚度∑D=5.2×105N/mm,柱轴压比大于0.4,楼层屈服强度系数为0.4,不小于相邻层该系数平均值的0.8。试问,在罕遇水平地震作用下,按弹性分析时作用于底层框架的总水平组合剪力标准值VEK(kN),最大不能超过下列何值才能满足规范对位移的限值要求?( )
提示:①按《建筑抗震设计规范》(GB 50011—2010)(2016年版)作答。
②结构在罕遇地震作用下薄弱层弹塑性变形计算可采用简化计算法;不考虑重力二阶效应。
③不考虑柱配箍影响。
根据《建筑抗震设计规范》(GB 50011—2010)(2016年版)表5.5.4可得,该框架结构12层,楼层屈服强度系数为:ξy为0.4。根据第5.5.2条第1款第2项可知,楼层屈服强度系数小于0.5,该结构应进行弹塑性变形验算。
根据第5.5.5条式(5.5.5)可知,最大弹塑性层间位移为:Δup≤[θp]h,θp为弹塑性层间位移角限值,可按表5.5.5采用取1/50。计算得:Δup≤(1/50)×6000=120mm。
根据式(5.5.4-1)可知,Δue=Δup/ηp。又ηp=2,因此Δue=120/2=60mm。
则底层框架的总水平组合剪力标准值为:VEk=∑Di·Δue=5.2×105×60=3.12×107N=3.12×104kN。