已知微分方程y’+y=f(x),其中f(x)是R上的连续函数.
(Ⅰ)若f(x)=x,求方程的通解.
(Ⅱ)若f(x)是周期为T的函数,证明:方程存在唯一的以T为周期的解.
【解】(Ⅰ)若f(x)=x,则方程为y'+y=x通解为
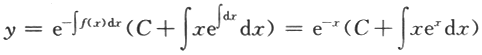
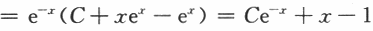
(Ⅱ)设y(x)为方程的任意解,则y'(x+T)+y(x+T)=f(x+T).
而f(x)周期为T,有f(x+T)=f(x).又y'(x)+y(x)=f(x).
因此y'(x+T)+y(x+T)-y'(x)-y(x)=0,有(e^x[y(x+T)-y(x)])'=0,
即e^x[y(x+T)=y(x)]=C.取C=0得y(x+T)-y(x)=0,
y(x)为唯一以T为周期的解.