在一块电路板的上下两端分别有n个接线柱。根据电路设计,用(i,π(i))表示将上端接线柱i与下端接线柱π(i)相连,称其为该电路板上的第i条连线。如图4-1所示的π(i)排列为{8,7,4,2,5,1,9,3,10,6}。对于任何1≤i<j≤n,第i条连线和第j条连线相交的充要条件是π(i)>π(j)。
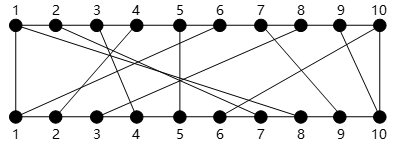
图4-1电路布线示意
在制作电路板时,要求将这n条连线分布到若干绝缘层上,在同一层上的连线不相交。现在要确定将哪些连线安排在一层上,使得该层上有尽可能多的连线,即确定连线集Nets={(i,π(i)),1≤i≤n}的最大不相交子集。
【分析问题】
记N(i,j)={t|(t,π(t))∈Nets,t≤i,π(t)≤j}。N(i,j)的最大不相交子集为MNS(i,j),size(i,j)=|MNS(i,j)|。
经分析,该问题具有最优子结构性质。对规模为n的电路布线问题,可以构造如下递归式:

【C代码】
下面是算法的C语言实现。
(1)变量说明
size[i][j]:上下端分别有i个和j个接线柱的电路板的第一层最大不相交连接数
pi[i]:π(i),下标从1开始
(2)C程序
#include"stdlib.h"
#include<stdio.h>
#define?N?10/*问题规模*/
int m=0;/*记录最大连接集合中的接线柱*/
void maxNum(int pi[],int size[N+1][N+1],int n){/*求最大不相交连接数*/
int i,j;
for(j=0;j<pi[1];j++)size[1][j]=0;/*当j<π(1)时*/
for(j=pi[1];j<=n;j++)(1);/*当j>=π(1)时*/
for(i=2;i<n;i++){
for(j=0;j<pi[i];j++)(2);/*当j<pi[i]时*/
for(j=pi[i];j<=n;j++){/*当j>=c[i]时,考虑两种情况*/
size[i][j]=size[i-1][j]>=size[i-1][pi[i]-1]+1?size[i-1][j]:size[i-1][pi[i]-1]+1;
}
}
/*最大连接数*/
size[n][n]=size[n-1][n]>=size[n-1][pi[n]-1]+1?size[n-1][n]:size[n-1][pi[n]-1]+1;
}
/*构造最大不相交连接集合,net[i]表示最大不相交子集中第i条连线的上端接线柱的序号*/
void constructSet(int pi[],int size[N+1][N+1],int n,int net[n]){
int i,j=n;
m=0;
for(i=n;i>1;i--){/*从后往前*/
if(size[i][j]!=size[i-1][j]){/*(i,pi[i])是最大不相交子集的一条连线*/
(3);/*将i记录到数组net中,连接线数自增1*/
j=pi[i]-1;/*更新扩展连线柱区间*/
}
}
if(j>=pi[1])net[m++]=1;/*当i=1时*/
}
【问题1】(6分)
根据以上说明和C代码,填充C代码中的空(1)~(3)。
【问题2】(6分)
据题干说明和以上C代码,算法采用了(4)算法设计策略。
函数maxNum和constructSet的时间复杂度分别为(5)和(6)(用O表示)。
【问题3】(3分)
若连接排列为{8,7,4,2,5,1,9,3,10,6},即如图4-1所示,则最大不相交连接数为(7),包含的连线为(8)(用(i,π(i))的形式给出)。
【问题1】
(1)size[1][j]=1
(2)size[i][j]=size[i-1][j]
(3)net[m++]=i;
【问题2】
(4)动态规划算法
(5)O(n2)
(6)O(n)
【问题3】
(7)4
(8)(3,π(3),(5,π(5)),(7,π(7)),(9,π(9))
或:(3,4),(5,5),(7,9),(9,10)
本题是算法设计题,涉及的算法策略是动态规划法。
【问题1】
本题要求补充代码,主要参照代码注释、题干的算法思路和递归式即可得到。
对于第(1)空,有注释“当j>=π(1)时”,此时属于i=1的其他情况,找到递归式的条件,所以(1)空填写size[1][j]=1;
对于第(2)空,有注释“当j<π(i)时”,此时属于i>1时,j<π(i)的条件,找到递归式对应条件,所以(2)空填写size[i][j]=size[i-1][j];
对于第(3)空,有注释“将i记录到数组net中,连接线数自增1”,将i记录到net数组,即net[]=i,其中net位置应该时连接线数m,此时为m++,因此(3)空填写net[m++]=i。本空也可以根据后面的代码推导。
【问题2】
1、根据题干描述“经分析,该问题具有最优子结构性质。对规模为n的电路布线问题,可以构造如下递归式”,根据最优子结构可判断本题使用的是动态规划法的算法策略。
2、根据代码,可以看到maxNum函数有两层嵌套循环,因此时间复杂度为O(n2)。
3、根据代码,可以看到constructSet函数只有一层循环结构,因此事件复杂度为O(n)。
【问题3】
这个是动态规划问题,不相交的平行线。
设a[i][j]为上端接线柱i与下端接线柱j前的最大不相交子集,则:
若i与j不相连,则i与j前的最大不想交子集等于i与j-1前或i-1与j前的最大不相交子集的最大值,即a[i][j]=max(a[i][j-1],a[i-1][j])
若i与j相连,则i与j前的最大不想交子集等于i-1与j-1前的最大不想交子集加1,即a[i][j]=a[i-1][j-1]+1
题目的意思就是要求出,没有交叉的这种连线的数量达到最大的情况。此时,有4条这样的线不会交叉,所以是大不相交子集连接数为4。如果你能找到5条这样不交叉的线,则是5。就这个意思。
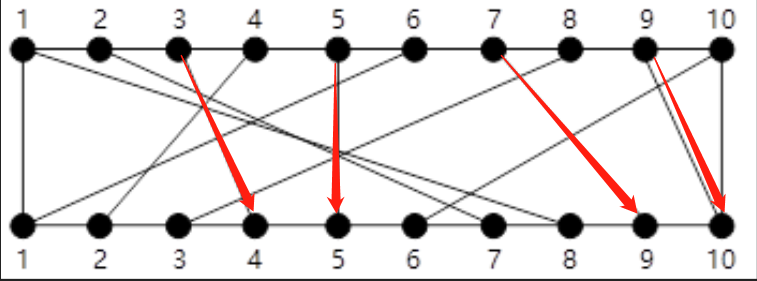
由此可得,最大不相交连接数为4,包含的连接线为:(3,π(3),(5,π(5)),(7,π(7)),(9,π(9))
( )is the process of transforming information so it is unintelligible to anyone but the intended recipient.
As each application module is completed,it undergoes( )to ensure that it operates correctly and reliably.
( )algorithm specifies the way to arrange data in a particular order.
After analyzing the source code,( )generates machine instructions that will carry out the meaning of the program at a later time.
( )can help organizations to better understand the information contained within the data and will also help identify the data that is most important to the business and future business decisions.
浏览器开启无痕浏览模式后,( )依然会被保存下来。
下列协议中,不属于TCP/IP协议簇的是( )。
下列传输介质中,带宽最宽、抗干扰能力最强的是( )。
数控编程常需要用参数来描述需要加工的零件的图形。在平面坐标系内,确定一个点需要2个独立的参数,确定一个正方形需要( )个独立的参数。
某书的页码为1,2,3,...,共用数字900个(一个多位数页码包含多个数字),据此可以推断,该书最大的页码为( )。