推荐等级：
发布时间： 2022-12-07 08:36
扫码用手机做题
甲、乙、丙、丁、戊、己、庚、辛是8名大学毕业生，其中己、庚、辛、丁是女性。现8人被分配往4所高校任教，每所学校分配2人。根据每人的授课能力绘制表格如下：
注:字母“A”代表授课能力优秀，字母“B”代表有基本的授课能力，字母“C”代表无法授课。
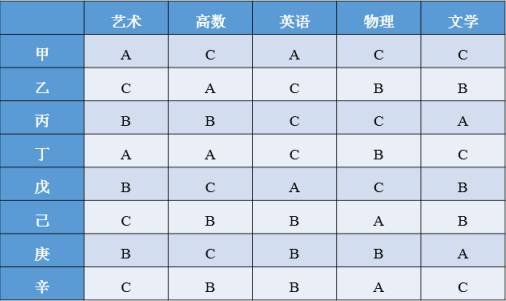
在5门课中，同时拥有哪两门课授课能力的大学毕业生是最多的?
本题解析：
第一步，确定题型。
题干具有匹配特征，确定为分析推理。
第二步，分析条件，进行推理。
根据表格可知，同时拥有艺术和英语、英语和文学、物理和文学授课能力的毕业生均有3人，同时拥有高数和物理授课能力的毕业生有4人。
因此，选择C选项。
甲、乙、丙、丁、戊、己、庚、辛是8名大学毕业生，其中己、庚、辛、丁是女性。现8人被分配往4所高校任教，每所学校分配2人。根据每人的授课能力绘制表格如下：
注:字母“A”代表授课能力优秀，字母“B”代表有基本的授课能力，字母“C”代表无法授课。
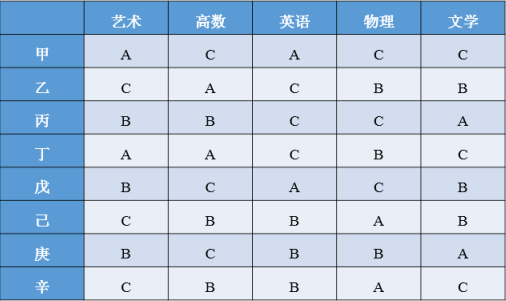
如将甲、乙、丙、丁四人集中安排在2所学校，则这2所学校中以下哪种情况可能发生?
本题解析：
第一步，确定题型。
题干具有匹配特征，确定为分析推理。
第二步，分析条件，进行推理。
A项：乙、丙、丁三人均无法教授英语，所以无论怎样分配都会有一所学校的英语无毕业生能教，该项不可能发生，排除；
B项：甲、乙、丙、丁四人的物理能力均不是优秀，所以无法做到每门课程都有优秀毕业生能教，该项不可能发生，排除；
C项：“每所学校都有优秀毕业生教授艺术”即甲和丁不在一所学校，进而文学的两个C不在一所学校，即“每所学校的文学都有毕业生能教”，该项正确；
D项：根据“每门科目都尽可能多的有优秀毕业生授课”，可知艺术均为优秀的甲、丁不在一所学校；又因为乙和丁的高数都是优秀，所以乙不能和丁在一所高校，最后可知：丁和丙在一所学校，甲和乙在一所学校，该项不可能发生，排除。
因此，选择C选项。
甲、乙、丙、丁、戊、己、庚、辛是8名大学毕业生，其中己、庚、辛、丁是女性。现8人被分配往4所高校任教，每所学校分配2人。根据每人的授课能力绘制表格如下：
注:字母“A”代表授课能力优秀，字母“B”代表有基本的授课能力，字母“C”代表无法授课。
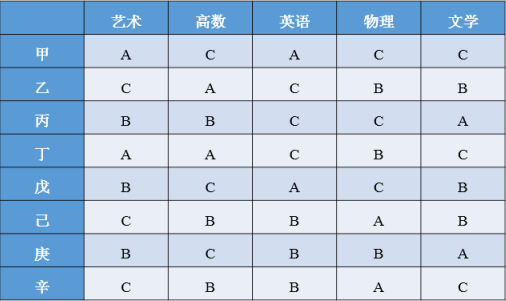
如将4名女性集中安排在2所学校，则所有学校中以下哪种情况不可能发生?
本题解析：
第一步，确定题型。
题干具有匹配特征，确定为分析推理。
第二步，分析条件，进行推理。
A项：若将甲和乙集中安排在同一所学校，那么该所学校的艺术、高数、英语都由授课能力优秀的毕业生授课，该项的情况可能发生；
B项：若将甲和戊集中安排在同一所学校，那么该所学校的高数和物理都没有毕业生会教，该项的情况可能发生；
C项：若将己和辛集中安排在同一所学校，那么两名毕业生对物理的授课能力都是优秀，该项的情况可能发生；
D项：甲、丙、戊的物理授课能力均为C，乙的物理授课能力为B，这4人不论如何搭配，都有一所学校没有毕业生能教物理，该项的情况不可能发生。
因此，选择D选项。
甲、乙、丙、丁、戊、己、庚、辛是8名大学毕业生，其中己、庚、辛、丁是女性。现8人被分配往4所高校任教，每所学校分配2人。根据每人的授课能力绘制表格如下：
注:字母“A”代表授课能力优秀，字母“B”代表有基本的授课能力，字母“C”代表无法授课。
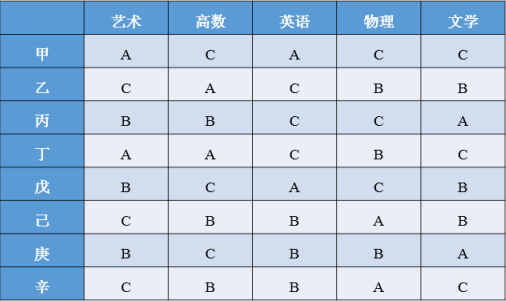
如果任教任务改为2所高校每所学校分配4人，则为了保证尽可能多的课程有优秀的授课效果，以下哪个安排是可行的?
本题解析：
第一步，确定题型。
题干具有匹配特征，确定为分析推理。
第二步，分析条件，进行推理。
根据表格数据可知，要想保证尽可能多的课程有优秀的授课效果，那么就需要尽可能将授课能力为A的科目不相同的毕业生分配到同一所学校。可按如下方式安排:
第一所学校:甲乙（丙己）/（丙辛）/（庚己）/（庚辛）。
第二所学校:丁戊（丙己）/（丙辛）/（庚己）/（庚辛）。
所以己和丁在同一所学校是可行的。
因此，选择B选项。
甲、乙、丙、丁、戊、己、庚、辛是8名大学毕业生，其中己、庚、辛、丁是女性。现8人被分配往4所高校任教，每所学校分配2人。根据每人的授课能力绘制表格如下：
注:字母“A”代表授课能力优秀，字母“B”代表有基本的授课能力，字母“C”代表无法授课。
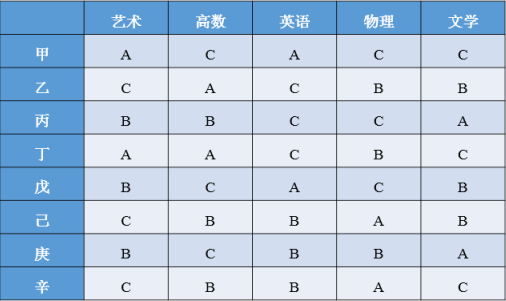
如果每所高校的2名大学毕业生要能教授所有5门课程，且甲和己被分到同一所高校，则与辛分到同一所高校的是：
本题解析：
第一步，确定题型。
题干具有匹配特征，确定为分析推理。
第二步，分析条件，进行推理。
根据题干可知，每所高校的2名毕业生要能教授所有5门课程，且辛的艺术和文学能力为C，那么与其搭档的毕业生艺术和文学能力不能为C，据此可排除乙和丁。已知甲和己被分到同一所高校，则辛的搭档只在能丙、戊、庚三人中选择。此时，如果辛的搭档是英语能力为A的戊或者英语能力为B的庚，则除了甲和己、辛和自己的搭档，剩下的4人中有3个人的英语能力为C，则定有1所高校的2名毕业生的英语能力都为C不满足题干要求。因此，辛只能与英语能力为C的丙搭档。
因此，选择D选项。
2021学年，S市共有普通高等学校64所，普通中等学校867所，普通小学680所，特殊教育学校31所。
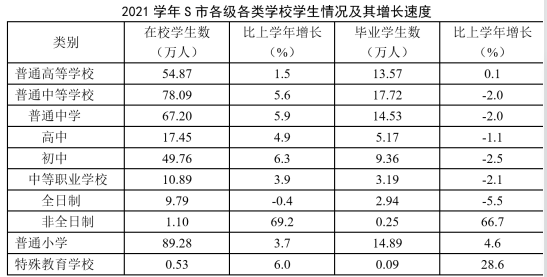
根据上述材料，下列说法正确的是：
本题解析：
第一步，本题考查综合分析，且需选出说法正确的一项。
第二步，A选项，减少量计算。定位表格材料，根据减少量计算n-1原则，2.0%=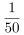
，S市普通中学毕业学生数减少量为
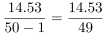＜0.3（万人），即减少不到3000人，错误。
B选项，现期平均数计算。定位文字和表格材料，根据平均数=
=
，平均每所学校在校学生数=
，故每所普通小学的在校学生数约为
≈0.13万人=1300人，错误。
C选项，基期量比较。定位表格材料，2021学年，S市四大类学校中毕业学生数最多的是普通中等学校（17.72万人）；根据基期量=
，观察四类学校较上学年的增速可知，仅普通中等学校负增长，故2020学年普通中等学校毕业学生数＞17.72万人，而其余三类学校毕业学生数均小于2021学年，则2020学年普通中等学校毕业学生人数必然大于其余三类学校，正确。
D选项，直接读数。定位表格材料，2021学年S市全日制中等职业学校在校生人数较上学年负增长，错误。
因此，选择C选项。
2021学年，S市共有普通高等学校64所，普通中等学校867所，普通小学680所，特殊教育学校31所。
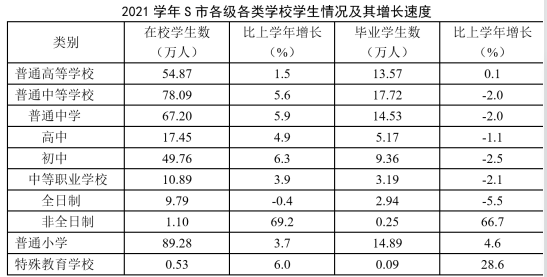
2021学年，普通小学在校学生数占S市各级各类学校总在校学生数的比重在以下哪个范围内？
本题解析：
第一步，本题考查现期比重计算中的求比重。
第二步，定位表格材料。
第三步，各级各类学校在校生数=普通高等学校+普通中等学校+普通小学+特殊教育学校，选项为范围，将最大数据从左向右截取前三位，其余数据舍相同处理，根据比重=
，代入数据可得所求比重约为
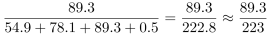≈40%，在C选项范围内。
因此，选择C选项。
2021学年，S市共有普通高等学校64所，普通中等学校867所，普通小学680所，特殊教育学校31所。
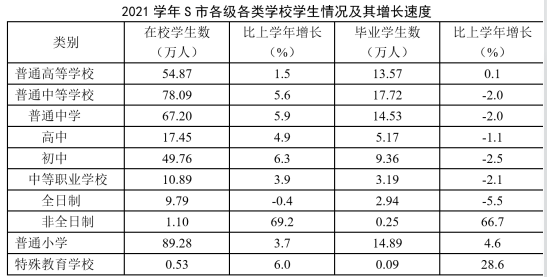
2021学年，S市下列各类学校在校学生数较上学年增长最多的是：
本题解析：
第一步，本题考查增长量公式比较。
第二步，定位表格材料。
第三步，根据增长量比较口诀“大大则大，一大一小看乘积”，普通中等学校的现期量和增长率（78.09，5.6%）均大于普通高等学校（54.87，1.5%），故增长量也高于普通高等学校，排除D选项。普通中等学校乘积（78.09×5.6%）＞普通小学乘积（89.28×3.7%）＞特殊教育学校乘积（0.53×6.0%），故普通中等学校同比增量最高。
因此，选择A选项。
试卷分类：行政职业能力测验
练习次数：5次
试卷分类：行政职业能力测验
练习次数：6次
试卷分类：行政职业能力测验
练习次数：5次
试卷分类：行政职业能力测验
练习次数：8次
试卷分类：行政职业能力测验
练习次数：5次
试卷分类：行政职业能力测验
练习次数：11次
试卷分类：行政职业能力测验
练习次数：13次
试卷分类：行政职业能力测验
练习次数：10次
试卷分类：行政职业能力测验
练习次数：9次
试卷分类：行政职业能力测验
练习次数：5次
=
，平均每所学校在校学生数=
，则所求倍数约为
≈86÷9≈9.5，与B选项最为接近。
，数据本身不大直接代入可得
≈11.76×
＞19.6，仅D选项符合。