中考数学2021年真题

试卷预览

1 计算题 1分

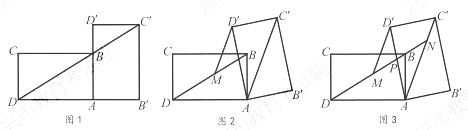
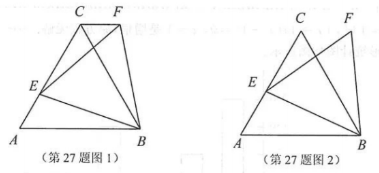
小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α( 0°<α≤90°),得到矩形AB"C'D'，连结 BD.

【探究1】如图1，当α =90°时，点C'恰好在DB延长线上．若AB=1，求BC的长.

【探究2】如图2,连结AC'，过点D'作 D'M// AC'交BD于点M．线段D'M与DM相等吗?请说明理由.

【探究3】在探究2的条件下，射线DB分别交AD'，AC'于点P，N（如图3)，发现线段DN，MN，PN存在一定的数量关系，请写出这个关系式，并加以证明.

查看答案 开始考试

正确答案：

本题解析：暂无解析

2 计算题 1分

已知二次函数y=-x²+6x-5

(1)求二次函数图象的顶点坐标.

(2）当1≤x≤4时,函数的最大值和最小值分别为多少?

(3）当t≤x≤t+3时，函数的最大值为m，最小值为n，若m-n =3，求t的值

查看答案 开始考试

正确答案：

本题解析：暂无解析

3 计算题 1分

某市为了解八年级学生视力健康状况，在全市随机抽查了400名八年级学生2021年初的视力数据，并调取该批学生2020年初的视力数据，制成如下统计图(不完整):

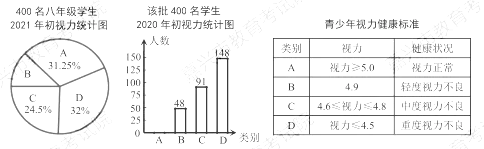
根据以上信息，请解答:

(1)分别求出被抽查的400名学生2021年初轻度视力不良(类别B）的扇形圆心角度数和2020年初视力正常（类别A②的人数.

(2）若2021年初该巿有八年级学生2万人，请估计这些学生2021年初视力正常的人数比2020年初增加了多少人?

(3）国家卫健委要求，全国初中生视力不良率控制在69%以内．请估计该市八年级学生2021年初视力不良率是否符合要求?并说明理由.

查看答案 开始考试

正确答案：

本题解析：暂无解析

4 计算题 1分

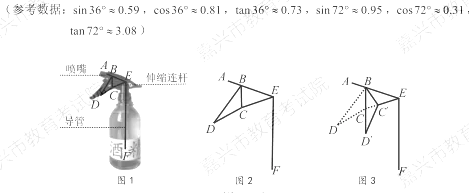
一酒精消毒瓶如图I，AB为喷嘴，△BCD为按压柄，CE为伸缩连杆，BE和EF为导管，其示意图如图2，∠DBE=∠BEF =108°,BD = 6 cm，BE=4cm.当按压柄△BCD按压到底时,BD转动到BD'，此时BD'//EF(如图3).

(1）求点D转动到点D'的路径长.

(2）求点D到直线EF的距离〔结果精确到0.1cm)

查看答案 开始考试

正确答案：

本题解析：暂无解析

5 计算题 1分

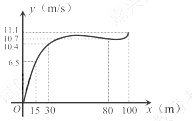
根据数学家凯勒的“百米赛跑数学模型”，前30米称为“加速期”，30米~80米为“中途期”.80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y (m/s)与路程x (m)之间的观测数据，绘制成曲线如图所示.

(1)y是关于x的函数吗?为什么?

(2)“加速期”结束时,小斌的速度为多少?

(3)根据右图提供的信息，给小斌提一条训练建议

查看答案 开始考试

正确答案：

本题解析：暂无解析

6 计算题 1分

如图，在7x7的正方形网格中，网格线的交点称为格点，点A，B在格点上，每一个小正方形的边长为1.

(1)以AB为边画菱形，使菱形的其余两个顶点都在格点上（画出一个即可)

(2)计算你所画菱形的面积

查看答案 开始考试

正确答案：

本题解析：暂无解析

7 计算题 1分

小敏和小霞两位同学解方程3(x-3)=(x-3)²的过程如下框：

你认为他们的解法是否正确?若正确请在框内打“√”若错误请在框内打“×”，并写出你的解答过程.

查看答案 开始考试

正确答案：

本题解析：暂无解析

8 计算题 1分

在数学兴趣小组活动中,小亮进行数学探究活动.

(1)△ABC是边长为3的等边三角形,E是边AC上的一点,且AE=1,小亮以BE为边作等边三角形BEF,如图1.求 CF的长;

(2)△ABC是边长为3的等边三角形,E是边AC上的一个动点,小亮以BE为边作等边三角形BEF,如图⒉在点E从点C到点A 的运动过程中,求点F所经过的路径长;

(3)△ABC是边长为3的等边三角形,M是高CD 上的一个动点,小亮以BM为边作等边三角形BMN,如图3.在点M从点C到点D的运动过程中,求点Ⅳ所经过的路径长;

(4)正方形ABCD的边长为3,E是边CB上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形BFGH ,其中点F,G都在直线AE上,如图4.当点E到达点B时,点F、G,H 与点B重合.则点H所经过的路径长为_▲_,点G所经过的路径长为_▲.

查看答案 开始考试

正确答案：

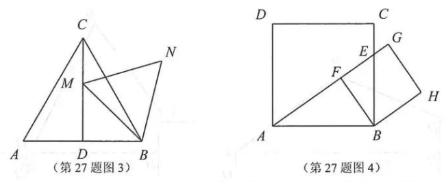
本题解析：暂无解析

9 计算题 1分

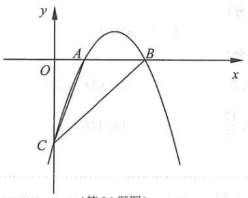
如图，抛物线y=mx²+(m²+3)x-(6m+9)与x轴交于点A，B，与y轴交于点C，已知B(3,0)

(1)求m的值和直线BC对应的函数表达式;

(2)P为抛物线上一点,若S△PBC=S△ABC,请直接写出点P的坐标;

(3)Q为抛物线上一点,若∠ACQ=45°,求点Q的坐标.

查看答案 开始考试

正确答案：

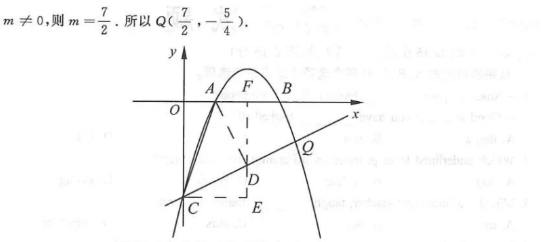
本题解析：暂无解析

10 计算题 1分

我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿AB摆成如图1所示.已知AB=4.8 m,鱼竿尾端A离岸边0.4 m,即 AD=0.4 m.海面与地面AD平行且相距1.2 m,即DH=1.2 m.

(1)如图1,在无鱼上钩时,海面上方的鱼线BC与海面HC 的夹角∠BCH=37°,海面下方的鱼线CO与海面HC垂直,鱼竿AB与地面AD的夹角∠BAD=22°.求点О到岸边DH的距离;

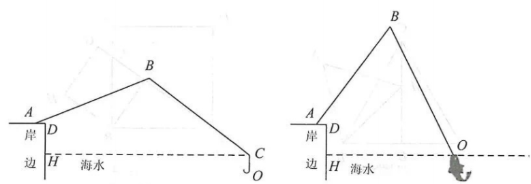
(2)如图2,在有鱼上钩时,鱼竿与地面的夹角LBAD=53°,此时鱼线被拉直,鱼线BO=5.46 m,点О恰好位于海面.求点О到岸边DH的距离.

查看答案 开始考试

正确答案：

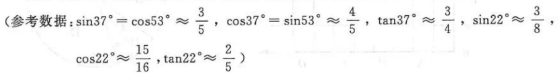
本题解析：暂无解析