推荐等级:
发布时间: 2021-12-20 07:54
扫码用手机做题
阅读下列说明和C++代码,将应填入( )处的字句写在答题纸的对应栏内。
【说明】
某图像预览程序要求能够查看BMP、JPEG和GIF三种格式的文件,且能够Windows和Linux两种操作系统上运行。程序需具有较好的扩展性以支持新的文件格式和操作系统。为满足上述需求并减少所需生成的子类数目,现采用桥接(Bridge)模式进行设计,得到如图5-1所示的类图。
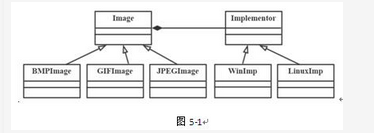
【C++代码】
#include<iostream>#include<:string>;Using namespace std;class Matrix{//各种格式的文件最终都被转化为像素矩阵//此处代码省略};class Implementor{public:( );显示像素矩阵 m};class WinImp:publicImplementor{public:Viod doPaint(Matrix m){/*调用 Windows 系统的绘制函数绘制像素矩阵*/};class LinuxImp:publicImplementor{/*调用 Linux 系统的绘制函数绘制像素矩阵*/}};class Image{public:viod setImp(Implement*imp) {this->imp=imp;}Virtual viod parseFile(string fileName)=0protected:Implementor*imp;};class BMPImage:publicImage{//此处省略代码};class GIFImage:publicImage{Public:viod parseFile(string fileName) {//此处解析 GIF 文件并获得一个像素矩阵对象 m( );显示像素矩阵 m}};class JPEGImage:publicImage{//此处代码省略};int main(){//在 linux 操作系统上查看 demo.gif 图像文件Image*image=( );Implementor*imageImp=( );( )Image->parseFile(〝demo.gif〝);return0;}
本题解析:
1.virtual void doPaint(Matrix m) = 0
2. imp->doPaint(m)
3. new GIFImage()
4. new LinuxImp()
5. image->setImp(imageImp)
阅读下列说明和C代码,回答问题1至问题2,将解答写在答题纸的对应栏内。
【说明】
一个无向连通图G点上的哈密尔顿(Hamiltion)回路是指从图G上的某个顶点出发,经过图上所有其他顶点一次且仅一次,最后回到该顶点的路径。哈密尔顿回路算法的基础如下:假设图G存在一个从顶点V0出发的哈密尔顿回路V1--V2--V3--...--Vn-1--V0。算法从顶点V0出发,访问该顶点的一个未被访问的邻接顶点V1,接着从顶点V1出发,访问V1一个未被访问的邻接顶点V2,..。;对顶点Vi,重复进行以下操作:访问Vi的一个未被访问的邻接接点Vi+1;若Vi的所有邻接顶点均已被访问,则返回到顶点Vi-1,考虑Vi-1的下一个未被访问的邻接顶点,仍记为Vi;直到找到一条哈密尔顿回路或者找不到哈密尔顿回路,算法结束。
【C代码】
下面是算法的C语言实现。
(1)常量和变量说明
n :图G中的顶点数
c[][]:图G的邻接矩阵
K:统计变量,当前已经访问的顶点数为k+1
x[k]:第k个访问的顶点编号,从0开始
Visited[x[k]]:第k个顶点的访问标志,0表示未访问,1表示已访问
(2)C程序
#include <stido.h>#include <stidb.h>#define MAX 100voidHamilton(intn,int x[MAX,intc[MAX][MAX]){int;int visited[MAX];int k;/*初始化 x 数组和 visited 数组*/for (i=0:i<n;i++){x[i]=0;visited [i]=0;}/*访问起始顶点*/k=0( );x[0]=0K=k+1/*访问其他顶点*/while(k>=0){x[k]=x[k]+1;while(x[k]<n){if ( )&&c[x[k-1]][x[k]==1){/*邻接顶点 x[k]未被访问过*/break;}else{x[k] = x[k] +1}}if(x[k] <n &&( ){ /*找到一条哈密尔顿回路*/for (k=0;k<n;k++){prinf(〝%d--〝,x[k] ; /*输出哈密尔顿回路*/}prinf(〝%d--〝,x[0] ;return;}elseif x[k]<n&&k<n-1){/*设置当前顶点的访问标志,继续下一个顶点*/( );k=k+1;}else{/*没有未被访问过的邻接顶点,回退到上一个顶点*/x[k]=0;visited x[k]=0;( );}}}
【问题1】(10分)
根据题干说明。填充C代码中的空(1)~(5)。
【问题2】(5分)
根据题干说明和C代码,算法采用的设计策略为( ),该方法在遍历图的顶点时,采用的
是( )方法(深度优先或广度优先)。
本题解析:
【问题1】(10分)
1. visited[0] = 1
2. visited[x[k]] == 0
3. k==n-1&&c[x[k]][x[0]==1
4. visited[x[k]] = 1
5. k = k - 1
【问题2】(5分)
回溯法、深度优先。
阅读以下说明和C程序,将应填入 (n) 处的字句写在对应栏内。3、【说明】下面的程序用DoleRob算法生成N阶(N为奇数)魔方阵(各行、列、对角线数字之和相等)。该算法的过程为:从1开始,按如下方法依次插入各自然数,直到N2为止。 a.在第一行的正中插入1。 b.新位置应当处于最近插入位置的右上方,若该位置已超出方阵的上边界,则新位置取应选列的最下一个位置;若超出右边界,则新位置取应选行的最左一个位置。 c.若最近插入的元素是N的整数倍,则选同列的下一行位置为新位置。 例如,3阶魔方阵如下所示: 8 1 6 3 5 7 4 9 2【C程序】 #include<stdio.h> #include<stdlib.h> #define SIZE 50 main( ) { int row, col, n,value; int a[SIZE+1][SIZE+1]; /*不使用下标为0的元素*/ printf("请输入要输出魔方阵的阶数n(奇数,<%d):n=",SIZE.; scanf("%d",&n); if (!(n % 2)||n < 1 || (1) ) { printf("输入数据有误!\n"); exit(0); } row=1; col = (n+1)/2; value=1; while(value< = (2) ) { a[row][col] = value; /*计算下一位置*/ if(value%n !=0){ row--; (3) ; if(row<1) row=n; if(col>n) (4) ; } else row++; value = (5) ; } printf("\n%d阶魔方阵如下所示:\n\n",n); for(row = 1;row <= n; row++){ for(col = 1; col <=n; col++) printf("%5d",a[row][col]); printf("\n"); } }
本题解析:
(1)n>SIZE,或其等价表示 (2)n*n (3)col++,或++col,或col=col+1,或其等价表示 (4)col-=n,或col=1,或其等价表示 (5)value+l,或其等价表示
【解析】
本题考查根据算法编写程序的基本能力。 N阶魔方阵定义为各行、列、对角线的数字之和相等。DoleRob给出了奇数阶魔方阵的算法,算法中方阵的行号和列号从1至N取值。程序中空(1)处判断n的合法性, n需为奇数,矩阵规模应不超过SIZE2。 根据题中的算法描述,由于要按次序将数值1~n2放入方阵中(在程序中以value表示每次要存入的数值),因此从1开始填入。将数值填入方阵的语句为“a[row][col]= value;”,该语句在循环中,因此循环条件为“value<=n*n”,因此,空(2)处填入“n*n”。 程序中,本次填入的数值为value的值,下一次要填入的数值为value加1,因此,空(5)处应填入“value+l”。 数值1的位置在第一行的正中间,即行号为1、列号为(n+1)/2,下一个位置即2的位置在1的右上方,即1所在位置的行号减1、列号加1。当新位置超出方阵的上边界,则新位置取应选列的最下一个位置:若超出右边界,则新位置取应选行的最左一个位置,因此对于3阶魔方阵,1填入第1行第2列,2填入第3行第3列,3填入第2行第1列,其余位置按照算法步骤b类推。因此,空(3)处填入“col++”或其等价形式,空(4)处填入“col=1或“col-=n”。需要考虑的特殊情况是本次填入的value值为N的倍数时,下一个插入位置为本次插入位置的正下方,即对于3阶矩阵,4填入3的正下方,7填入6的正下方等。
阅读下列说明和Java代码,将应填入( )处的字句写在答题纸的对应栏内。
【说明】
某图像预览程序要求能够查看BMP、JPEG和GIF三种格式的文件,且能够在Windows和Linux两种操作系统上运行。程序需具有较好的扩展性以支持新的文件格式和操作系统。为满足上述需求并减少所需生成的子类数目,现采用桥接模式进行设计,得到如图6-1所示的类图。
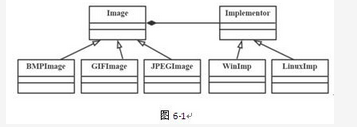
【Jave代码】
Import java.util.*;class Matrix{ //各种格式的文件最终都被转化为像素矩阵//此处代码省略};abstract class Implementor{Public( );//显示像素矩阵 m};class WinImp extends Implementor{public void doPaint(Matrix m){//调用Windows 系统的绘制函数绘制像素矩阵}};class LinuxImp extends Implementor{public void doPaint(Matrix m){//调用Linux 系统的绘制函数绘制像素矩阵}};abstract class Image{public void setImp(Implementor imp){this.imp= imp; }public abstract void parseFile(String fileName);protected Implementor imp;};class BMPImage extends Image{//此处代码省略};class GIFImage extends Image{public void parseFile(String fileName) {//此处解析BMP 文件并获得一个像素矩阵对象 m( );//显示像素矩阵 m}};Class Main{Public static viod main(String[]args){//在Linux 操作系统上查看 demo.gif 图像文件Image image=()Implementor imageImp=()( )Image.parseFile(〝demo.gif〝);}}
本题解析:
1. abstract void doPaint(Matrix m)
2. imp.doPaint(m)
3. new GIFImage()
4. new LinuxImp()
5. image.setImp(imageImp)
阅读以下C++代码,填充(1)~(5)的空缺,将解答填入答题纸的对应栏内。【说明】在下面程序横线处填上适当的字句,使其输出结果为:x=5x=6y=7x=8z=9【程序】#include<iostream.h>class X1{int x;(1):X1(int xx=0){x=xx;}(2)void Output()(cout<<"x="<<x<<end;}};(3)Y1:public X1{int y;public:Y1(int xx=0,int yy=0):X1(xx){y=yy;}(2)void Output(){(4)Output();cout<<"y="<<y<<end1;}};class Z1:pubtic X1{int z:(5):Z1(int xx=0,int zz=0):X1(xx){z=zz;}②void Output(){X1::Output();cout<<"z="<<z<<end1;}};void main(){X1 a(5);Y1 b(6,7);Z1 c(8,9);X1*p[3]={&a,&b,&c};For(int i=0;i<3;i++){p[i]-->Output();cout<<end1;}}
本题解析:
(1)public
(2)virtual
(3)class
(4)X1::
(5)public
【解析】
通过对比三个类的定义就可以发现,在类X1和Z1的定义中缺少类的成员属性声明,而类一般将成员变量声明为公有的、私有的或受保护的三种类型中的一种,在类的定义中,我们一般将类的构造函数放在公有的属性下面,在题目中只能选择公有的属性了,因此,第1空和第5空中应该填“public”。对三个类的定义进行仔细观察后,我们同样可以发现,每个类中都定义了一个同名函数Output(),而且在后两个类的函数体中调用了函数Output(),由此,我们应该想到虚函数。虚函数的作用是允许在派生类中重新定义与基类同名的函数,并且可以通过基类指针或引用来访问基类和派生类中的同名函数。因此,第2空应该填“virtual”。第3空就简单了,考查类的定义,应该填类的标识符“class”。从程序中我们可以看到,类Y1和Z1都以公有的方式继承类X1。从输出的结果来分析,类Y1和Z1都输出了两个数,但单从类Z1的函数来看,只能输出一个变量的值z,因此,可以发现在类Z1中应该和类Y1一样,都调用了类X1的函数Output(),因此,第4空的答案为“X1::”。
试卷分类:高级信息系统项目管理师
练习次数:0次
试卷分类:高级系统架构设计师
练习次数:0次
试卷分类:中级系统集成项目管理工程师
练习次数:0次
试卷分类:中级信息系统监理师
练习次数:0次
试卷分类:中级软件设计师
练习次数:0次
试卷分类:高级网络规划设计师
练习次数:0次
试卷分类:高级网络规划设计师
练习次数:0次
试卷分类:高级网络规划设计师
练习次数:0次
试卷分类:中级网络工程师
练习次数:0次
试卷分类:中级网络工程师
练习次数:0次