2012年上半年（上午）《软件设计师》真题

试卷预览

1 单选题 1分

以下关于网络中各种交换设备的叙述中，错误的是（　　）。

查看答案 开始考试

正确答案：C

本题解析：

交换机有多种，共同的特点都是根据某种标识把输入数据包交换到输出端口。以太网交换机根据MAC地址进行交换：帧中继交换机根据虚电路号DLCI进行交换：Internet中使用的三层交换机根据IP地址进行转发，并根据MAC地址进行交换：ATM交换机根据虚电路标识VPI和VCI进行交换。

2 单选题 1分

现要对n个实数（仅包含正实数和负实数）组成的数组A进行重新排列，使得其中所有的负实数都位于正实数之前。求解该问题的算法的伪代码如下所示，则该算法的时间和空间更杂度分别为（　　）。

i=0;j=n-1;

while i＜j do

while A[i]＜0 do

i=i+1;

while A[j]>0 do

j=j-1;

if i＜j do

交换A[i]和A[j];

问题1选项

查看答案 开始考试

正确答案：C

本题解析：

根据程序不难看出，要将负实数位于正实数之前，其实就是对所有元素进行了一次遍历，正实数和负实数互换位置即可，因此其时间复杂度为O（n），由于元素A[i]和A[j]互换时，需要一个临时存储空间来存放元素，因此其空间复杂度为O（1）。

3 单选题 1分

若n2、n1、n0分别表示一个二叉树中度为2、度为1和叶子结点的数目（结点的度定义为结点的子树数目），则对于任何一个非空的二叉树，（　　）。

查看答案 开始考试

正确答案：D

本题解析：

根据二叉树的性质，我们知道n0=n2+1，因此在一棵二叉树中，叶子结点的数目一定是大于度为2的结点的个数。

4 单选题 1分

在字符串的KMP模式匹配锋法中，需要求解模式串p的next函数值，其定义如下所示。若模式串p为“aaabaaa”，则其next函数值为（　　）。

查看答案 开始考试

正确答案：A

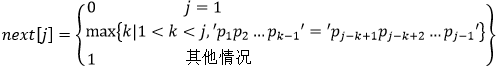
本题解析：

KMP模式匹配算法通俗点说就是一种在一个字符串中定位另一个串的高效算法。其实我们在做这个题目时，也可以不需要知道KMP模式匹配算法，可以根据题目给出的定义式来求解。

【对于本题公式】

1、当j=1时，由（1）式，next[1]=0；

2、当j!=1时，由（2）式，max{k|1＜k＜j'p1p2...pk-1'='pj-k+1pj-k+2...pj-1'}，即选择符合要求的最大k值，要求：1＜k＜j，并且满足'p1p2...pk-1'='pj-k+1pj-k+2...pj-1'，如果有满足要求的k值，则next[j]=max{k}；如果找不到满足条件的k值，则由（3）式next[j]=1。

3、取值范围，j、k都为正整数，且1＜=j＜=5

【求取next[]过程如下】

1、当j=1时，由（1）式，next[1]=0；

2、当j=2时，找不到满足1＜k＜j的数k，由（3）式，next[2]=1;

3、当j=3时，满足1＜k＜j的数k=2，同时需要满足'p1p2...pk-1'='pj-k+1pj-k+2...pj-1'。'p1p2...pk-1'='p1p2...p1'=p1，为第一个字母a；'pj-k+1pj-k+2...pj-1'='p2p3...p2'=p2，为第二个字母a，此时，k满足条件，由（2）式，next[3]=k=2。

4、当j=4时，满足1＜k＜j的数k=2或3：

（1）当k=2，'p1p2...pk-1'='p1p2...p1'=p1，为第一个字母a，'p1p2...pk-1'='p3p4...p3'=p3，为第三个字母a，满足'p1p2...pk-1'='pj-k+1pj-k+2...pj-1'。

（2）当k=3，'p1p2...pk-1'='p1p2...p2'=p1p2，为第一二字母aa，'pj-k+1pj-k+2...pj-1'='p2p3...p3'=p2p3，为第二三个字母aa，'p1p2...pk-1'='pj-k+1pj-k+2...pj-1'。

因此next[4]=max{2，3}=3。

5、j=5，满足1＜k＜j的数k=2、3或4：

（1）当k=2，'p1p2...pk-1'='p1p2...p1'=p1，为第一个字母a，'p1p2...pj-1'='p4p5...p4'=p4，为第四个字母b，不满足'p1p2...pk-1'='pj-k+1pj-k+2...pj-1'。

（2）当k=3，'p1p2...pk-1'='p1p2...p2'=p1p2，为第一二字母aa，'pj-k+1pj-k+2...pj-1'='p3p4...p4'=p3p4，为第三四个字母ab，不满足'p1p2...pk-1'='pj-k+1pj-k+2...pj-1'。

（3）当k=4，'p1p2...pk-1'='p1p2Lp3'=p1p2p3，为第一二三字母aaa，'pj-k+1pj-k+2...pj-1'='p2p3...p4'=p2p3p4，为第二三四个字母aab，不满足'p1p2...pk-1'='pj-k+1pj-k+2...pj-1'。

因此，当j=5时，没有满足条件k，此时由（3）式，next[5]=1。

同理我们可以求得当j=6，j=7的结果，本题正确答案选A。

5 单选题 1分

对于一个长度大于1且不存在重复元素的序列，令其所有元素依次通过一个初始为空的队列后，再通过一个初始为空的栈。设队列和栈的容量都足够大，一个序列通过队列（栈）的含义是序列的每个元素都入队列（栈）且出队列（栈）一次且仅一次。对于该序列在上述队列和栈上的操作，正确的叙述是（　　）。

查看答案 开始考试

正确答案：C

本题解析：

本题主要考查队列和栈的特性。队列具有先进先出的特点，而栈具有后进先出的特点。因此我们可以知道入队序列与出队序列一定相同，但入栈序列与出栈序列不一定相同。比如a，b，c这样一个序列，那么按照a，b，c的顺序入队列，那么其出队列的次序一定是a，b，c。而按照a，b，c的顺序入栈，那么可能是a入栈后就出栈，然后b入栈又出栈，然后C入栈出栈。也可能是等a，b，c都入栈后再出栈，那么出栈序列就是c，b，a。

6 单选题 1分

函数（过程）调用时，常采用传值与传地址两种方式在实参与形参间传递信息。以下叙述中，正确的是（　　）。

查看答案 开始考试

正确答案：D

本题解析：

形式参数就是过程定义中函数名后括号中所带的参数；实际参数是在调用点表示向被调用过程传递的数据。

在函数调用时，数据传递的方向是从实参到形参。只是采用传值传递方式时，传递的是数值，这个数值只要是确定的即可，可以是常量、变量或表达式等。而采用传址传递方式时，传递的是地址，因此实参必须有地址。

7 单选题 1分

E-R模型向关系模型转换时，三个实体之间多对多的联系m:n:p应该转换为一个独立的关系模式，且该关系模式的关键字由（　　）组成。

查看答案 开始考试

正确答案：B

本题解析：

在E-R模型向关系模型转换时，如果是多对多的联系，那么这个联系需要转换为一个独立的关系模式，且该关系模式的属性由各实体的关键字和该联系自身的属性组成，而该关系模式的关键字（主键）由各实体的关键字组成。

8 单选题 1分

下图所示为一个有限自动机（其中，A是初态、C是终态），该自动机所识别的字符串的特点是（　　）。

查看答案 开始考试

正确答案：C

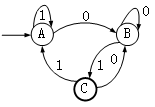
本题解析：

被有限自动机所识别是指从初态开始到终态结束，所输入的字符串能够按顺序地执行下去，若到某个状态不能往下走得到下一个字符，则认为不能识别。

在本题中，从初态A出发，不管经过多少个1和0之后，只能是处在A、B、C三种状态中的一种，所以在(0|1)*后，只能是处在A、B、C三种状态中的一种，不管是在那个状态，输入0后，都会处在状态B，然后输入1，都会转换到状态C，因此与本题有限自动机等价的正规式是(0|1)*01，即该自动机所识别的字符串的特点是必须以01结尾的0、1串。

9 单选题 1分

设计模式根据目的进行分类，可以分为创建型、结构型和行为型三种。其中结构型模式用于处理类和对象的组合。（　　）模式是一种结构型模式。

查看答案 开始考试

正确答案：A

本题解析：

常见的创建型模式主要有工厂方法（FactoryMethod）、抽象工厂（AbstractFactory）、单例（Singleton）、构建器（Builder）、原型（Prototype）模式；结构型模式有适配器（Adapter）、组合（Composite）、装饰（Decorator）、代理（Proxy）、享元（Flyweight）、外观（Fa?ade）、桥接（Bridge）模式；行为型模式有策略（Strategy）、模板方法（TemplateMethod）、迭代器（Iterator）、责任链（ChainofResponsibility）、命令（Command）、备忘录（Memento）、状态（State）、访问者（Visitor）、解释器（（Interpreter）、中介者（Mediator）、观察者（Observer）模式。

10 单选题 1分

根据ISO/IEC9126软件质量模型中对软件质量特性的定义，可维护性质量特性的（　　）子特性是指与为确认经修改软件所需努力有关的软件属性。

查看答案 开始考试

正确答案：A

本题解析：

可维护性质量特性是指与软件维护的难易程度相关的一组软件属性，它包含了易分析性、稳定性、易测试性和易改变性4个子特性。其中：

易分析性是描述诊断缺陷或失效原因、判定待修改程度的难易程度的特性。

稳定性是描述修改造成难以预料的后果的风险程度，风险程度越低，稳定性越好。

易测试性是描述测试已修改软件的难易程度的特性。

易改变性是描述修改、排错或适应环境变化的难易程度。

本题中，是说与为确认经修改软件所需努力有关的软件属性，也就是说要确认修改后的软件是否正确所要付出的努力，这应该是易测试性所描述的内容，因此本题答案选A。