2011年下半年（上午）《软件设计师》真题

试卷预览

1 单选题 1分

在Windows系统中，为排除DNS域名解析故障，需要刷新DNS解析器缓存，应使用的命令是（　　）。

查看答案 开始考试

正确答案：B

本题解析：

ipconfig/renew的含义是更新所有适配器的 DHCP 配置。该命令仅在具有配置为自动获取 IP 地址的适配器的计算机上可用。

ipconfig/flushdns的含义是刷新并重设DNS解析器缓存。

netstat –r用于显示核心路由表。

arp –a用于查看ARP高速缓存中的内容。

2 单选题 1分

设算法A的时间复杂度可用递归式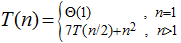表示，算法B的时间复杂度可用递归式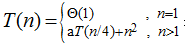表示，若要使得算法B渐进地快于算法A，则a的最大整数为（　　）。

查看答案 开始考试

正确答案：A

本题解析：

题目要求使得算法B渐进地快于算法A，即B的时间复杂度小于A的时间复杂度。

对算法A进行简单的化简，令n=n/2，我们可以得到算法A的T(n)=49T(n/4)+11/4n2；

而算法B的T(n)=aT(n/4)+n2，而根据渐进的规则，算法A的时间复杂度应该为49T(n/4)，而算法B的时间复杂度应该为aT(n/4)，因此a的取值应该要小于49，本题只有A选项符合。

3 单选题 1分

在有n个无序无重复元素值的数组中查找第i小的数的算法描述如下：任意取一个元素r，用划分操作确定其在数组中的位置，假设元素r为第k小的数。若i等于k，则返回该元素值；若i小于k，则在划分的前半部分递归进行划分操作找第i小的数；否则在划分的后半部分递归进行划分操作找第k-i小的数。该算法是一种基于（　　）策略的算法。

查看答案 开始考试

正确答案：A

本题解析：

分治法：对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决；否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。本题的算法思想是分治法的思想。

动态规划法：这种算法也用到了分治思想，它的做法是将问题实例分解为更小的、相似的子问题，并存储子问题的解而避免计算重复的子问题。

贪心算法：它是一种不追求最优解，只希望得到较为满意解的方法。贪心算法一般可以快速得到满意的解，因为它省去了为找到最优解而穷尽所有可能所必须耗费的大量时间。贪心算法常以当前情况为基础做最优选择，而不考虑各种可能的整体情况，所以贪心算法不要回溯。

回溯算法（试探法）：它是一种系统地搜索问题的解的方法。回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。其实现一般要用到递归和堆栈。

4 单选题 1分

一棵满二叉树，其每一层结点个数都达到最大值，对其中的结点从l开始顺序编号，即根结点编号为1，其左、右孩子结点编号分别为2和3，再下一层从左到右的编号为4、5、6、7，依此类推，每一层都从左到右依次编号，直到最后的叶子结点层为止，则用（　　）可判定编号为m和n的两个结点是否在同一层。

查看答案 开始考试

正确答案：B

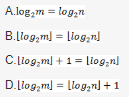
本题解析：

如果是满二叉树，那么其第n层的结点数应该是第n-1层结点数的两倍，从根（第一层）开始，各层的结点数应分别是2n-1个，其中n为当前的层次，因此一颗x层的满二叉树，其总的结点数位2x-1个。而如果知道结点编号m，我们可以用log2m+1来求取该结点属于那一层，同样，对于编号为n的结点，所属层次为log2n+1，两者属于同一层次则应该满足log2m+1=log2n+1，因此B选项log2m=log2n符合要求。

5 单选题 1分

无向图中一个顶点的度是指图中与该顶点相邻接的顶点数。若无向图G中的顶点数为n，边数为e，则所有顶点的度数之和为（　　）。

查看答案 开始考试

正确答案：D

本题解析：

在无向图中，一条边连接两个顶点，即如果存在一条边，那么与这条边相关的两个顶点的度都为加1，那么总的度就应该加2，因此，如果图中有n条边，那么所有顶点的度数之和就应该为2e。

6 单选题 1分

对于线性表（由n个同类元素构成的线性序列），采用单向循环链表存储的特点之一是（　　）。

查看答案 开始考试

正确答案：A

本题解析：

采用单向循环链表存储的特点之一是从表中任意结点出发都能遍历整个链表，另外便于元素的元素节点的删除与插入。如需要对表中的任意节点进行随机访问需采用顺序存储结构。

7 单选题 1分

在KMP模式匹配算法中，需要求解模式串p的next函数值，其定义如下（其中，j为模式串中字符的序号）。对于模式串“abaabaca”，其next函数值序列为（　　）。

查看答案 开始考试

正确答案：B

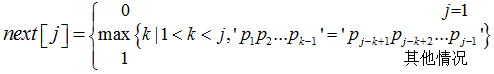
本题解析：

KMP模式匹配算法通俗点说就是一种在一个字符串中定位另一个串的高效算法。其实我们在做这个题目时，也可以不需要知道KMP模式匹配算法，可以根据题目给出的定义式来求解。

当j=1时，很显然next[1]=0。

当j=2时，由于1＜k＜j，因此k无法取到合适值，因此next[2]=1。

当j=3时，k的取值为2，那么等号左边的‘P1P2…PK-1’字符串就是P1，为字符串中的第一个字符 a，而右边就是P2，即字符串中的第二个字符b，显然，它们不相等，因此next[3]=1。

当j=4时，k可以取值2或者3，取值为2时，等号左边为第一个字符a，而等号右边为 P3，也是字符a，因此相等，但这个时候我们还要判定当k取值为3时，等号左边为第一与第二个字符，即‘ab’，而右边为‘ba’，显然不相等，因此next[4]=2。

同理我们可以求得当j=5，j=6的结果，本题正确答案选B。

8 单选题 1分

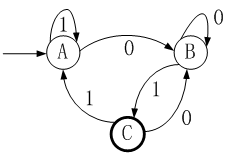
下图所示为一个有限自动机（其中，A是初态、C是终态），该自动机识别的语言可用正规式（　　）表示。

查看答案 开始考试

正确答案：A

本题解析：

被有限自动机所识别是指从初态开始到终态结束，所输入的字符串能够按顺序地执行下去，若到某个状态不能往下走得到下一个字符，则认为不能识别。

在本题中，选项A能被识别。从初态A出发，不管经过多少个1和0之后，只能是处在A、B、C三种状态中的一种，所以在(0|1)*后，只能是处在A、B、C三种状态中的一种，不管是在那个状态，输入0后，都会处在状态B，然后输入1，都会转换到状态C，因此选项A能被该有限自动机所识别。

同样的道理，我们可以知道其它选项的正规式不能被识别。

9 单选题 1分

欲动态地给一个对象添加职责，宜采用（　　）模式。

查看答案 开始考试

正确答案：D

本题解析：

适配器模式将一个接口转换成为客户想要的另一个接口，适配器模式使接口不兼容的那些类可以一起工作。

桥接模式将抽象部分与实现部分分离，使得它们两部分可以独立地变化。

组合模式组合多个对象形成树型结构以表示整体—部分的结构层次。

装饰器模式动态地给一个对象增加其他职责，就增加对象功能来说，装饰模式比生成子类实现更为灵活。

10 单选题 1分

在面向对象软件开发中，封装是一种（　　）技术，其目的是使对象的使用者和生产者分离。

查看答案 开始考试

正确答案：B

本题解析：

面向对象系统中的封装单位是对象，对象之间只能通过接口进行信息交流，对象外部不能对对象中的数据随意地进行访问。封装是一种信息隐藏技术，目的是使对象的定义和实现分离，这样，就能减少耦合，类内部的实现可以自由改变而不会影响其他的类或对象。