当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->高中“函数概念”(第一节课)设定的教学目标如下:①通过丰富实
高中“函数概念”(第一节课)设定的教学目标如下:
①通过丰富实例,进一步体会函数是描绘变量之间的依赖关系的重要数学模型,体会数学应用的广泛性:体会函数的实质是两个集合间的特殊对应关系;
②理解函数表达形式的多样性
③理解函数的定义。
完成下列设计,并且回答问题:
(1)根据教学目标①②,至少设计三个实例,并说明设计意图。
(2)根据教学目标③,至少设计两个例题.并说明设计意图。
(3)本节函数概念教学与初中函数概念教学有什么不同 本节课教学的重点、难点各是什么 请说明理由。
(1)实例一:自由落体运动 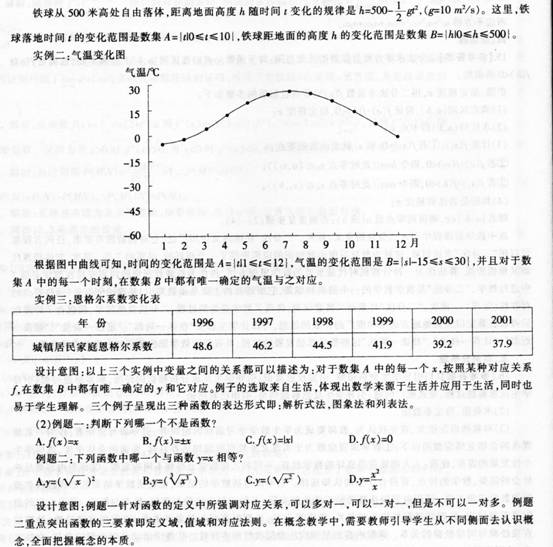
(3)高中函数概念与初中概念相比更具有一般性。实际上,高中的函数概念与初中的函数概念本质上是一 致的。不同点在于,表述方式不同——高中明确了集合、对应的方法。初中虽然没有明确定义域、值域这些集合,但这是客观存在的,也已经渗透了集合与对应的观点。与初中相比,高中引入了抽象的符号f(x)。f(x)指集合B中与x对应的那个数。当x确定时,f(x)也唯一确定。另外,初中并没有明确函数值域这个概念。
教学重点:在研究已有函数实例的过程中,感受在两个数集A,日之间所存在的对应关系厂,进而用集合、对应的语言刻画这一关系,获得函数概念。然后再进一步理解它。
教学难点:对抽象符号y=f(x)的理解。
教学重难点设置理由:函数是中学数学的核心概念,而函数概念的核心是“对应”,正确理解函数的概念是基础。从具体到抽象才符合学生在学习的过程中从感知到理解,从表象到概念的认识规律。抽象符号在数学中广泛使用,因此对于它的理解是难点也是重点。
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )

案例:
在有理数运算的课堂教学片段中,某学生的板演如下:

针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。

请分析例题1、例题2中每一步运算的依据。(10分)
初中数学课程是一门国家课程,其主要内容包括课程目标、教学内容、教学过程和( )等
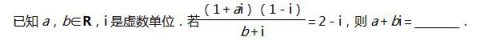
教师职业道德区别于其他职业道德的显著标志就是( )。
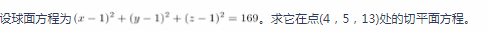
对高中数学的评价,下列说法错误的是( )。
