当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->所谓模型思想,就是根据特定的研究目的,采用形式化的数学语言,
所谓模型思想,就是根据特定的研究目的,采用形式化的数学语言,去抽象地、概括地表征所研究对象的主要特征、关系所形成的一种数学结构。在义务教育阶段数学中,用字母、数字及其他数学符号建立起来的代数式、关系式、方程、函数、不等式,及各种图表、图形等都是数学模型。
(1)请简述义务教育阶段建立和求解模型的过程:
(2)举一个运用模型思想解决实际问题的实例。
(1)建立和求解模型的过程包括:从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,求出结果、并讨论结果的意义。
(2)举例:某农户想利用一只1350的墙角砌一直角梯形鸡舍,现有一批可砌l0米长墙的砖块,试问BC为何值时才能使鸡舍面积最大。
本题可以设BC=x,则CD=10-x,再利用梯形的面积公式和几何知识,设梯形的面积为y,建立二次函数模型,找出x的取值范围,求函数的最大值即可解。 @jin
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )

案例:
在有理数运算的课堂教学片段中,某学生的板演如下:

针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。

请分析例题1、例题2中每一步运算的依据。(10分)
初中数学课程是一门国家课程,其主要内容包括课程目标、教学内容、教学过程和( )等
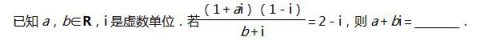
教师职业道德区别于其他职业道德的显著标志就是( )。
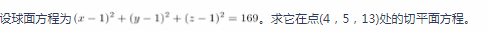
对高中数学的评价,下列说法错误的是( )。
