在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是(请作答此空)。
对于第一空,本题使用是分治法。1、分治法特征:对于一个规模为n问题,若该问题可以容易地解决(比如说规模n较小)则直接解决;否则将其分解为k个规模较小子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题解合并得到原问题解。2、动态规划法:在求解问题中,对于每一步决策,列出各种可能局部解,再依据某种判定条件,舍弃那些肯定不能得到最优解局部解,在每一步都经过筛选,以每一步都是最优解来保证全局是最优解。本题情景没有列出所有可能解进行筛选,因此,本题不属于动态规划法。3、回溯法:回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当搜索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择。这种走不通就退回再走技术就是回溯法。本题情景没有探索和回退过程,因此,本题不属于回溯法。4、贪心法:总是做出在当前来说是最好选择,而并不从整体上加以考虑,它所做每步选择只是当前步骤局部最优选择,但从整体来说不一定是最优选择。由于它不必为了寻找最优解而穷尽所有可能解,因此其耗费时间少,一般可以快速得到满意解,但得不到最优解。在本题情景中,没有给出每步选择局部最优判断条件,因此,本题属于贪心法。 由于本题算法过程,是依次与各个房子进行判断,当所有房子都被比较之后,则问题结束,因此时间复杂度与房子个数相关,本问题时间复杂度应该趋于现象,为O(n),属于贪心算法。对于第三空,关于对应序列(10,20,30,35,60,80,160,210,260,300)第一轮放置:在第一座房子x=10右侧20米处安装一个消防栓,可以覆盖10,20,30,35这4栋房子;2、第二轮放置:去掉前4栋房子,在第5栋房子x=60右侧20米处安装一个消防栓,可以覆盖60、80这2栋房子;3、第三轮放置:去掉前面已覆盖房子,在第7栋房子x=160右侧20米处安装一个消防栓,只可以覆盖160这一栋房子;4、第四轮放置:去掉前面已覆盖房子,在第8栋房子x=210右侧20米处安装一个消防栓,可以覆盖210这一栋房子第五轮放置:去掉前面已覆盖房子,在第9栋房子x=260右侧20米处安装一个消防栓,可以覆盖260、300这2栋房子;房子全部覆盖完毕,因此共需安装5个消防栓。对于第四空,对于得到一个最优解是动态规划特点,可以得到问题所有最优解,是回溯法特征,可以排除A、B选项。对于C、D选项。A.肯定可以求得问题一个最优解B.可以求得问题所有最优解C.对有些实例,可能得不到最优解D.只能得到近似最优解
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是(请作答此空)。
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装(请作答此空)个消防栓。以下关于该求解算法叙述中,正确是( )。
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为(请作答此空)。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是( )。

在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为(请作答此空);对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是( )。
阅读以下说明和流程图,填补流程图中空缺。 【说明】 设有整数数组A[1:N](N小于1),其元素有正有负。下面流程图在该数组中寻找连续排列若干个元素,使其和达到最大值,并输出其起始下标K、元素个数L以及最大和值M。 例如,若数组元素依次为3,-6,2,4,-2,3,-1,则输出K=3,L=4,M=7。该流程图中考察了A[1:N]中所有从下标i到下标j(j≥i)各元素之和S,并动态地记录其最大值M。【流程图】
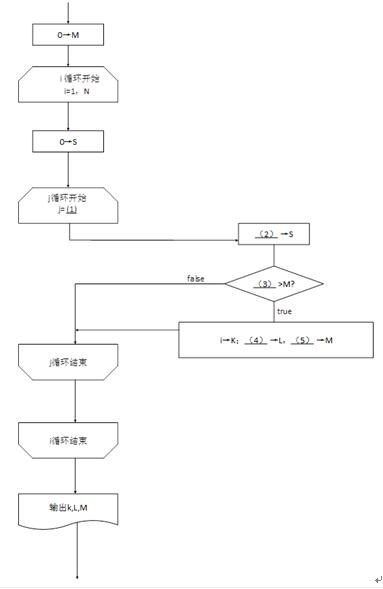
注:循环开始框内应给出循环控制变量初值和终值,默认递增值为1,格式为:循环控制变量=初值,终值
阅读下列说明和 Java代码,将应填入(n)处字句写在答题纸对应栏内。【说明】某航空公司会员积分系统将其会员划分为:普卡 (Basic) 、银卡(Silver)和金卡 (Gold)三个等级。非会员 (NonMember)可以申请成为普卡会员。会员等级根据其 一年内累积里程数进行调整。描述会员等级调整状态图如图 6-1 所示 。现采用状态 (State) 模式实现上述场景,得到如图 6-2 所示类图。
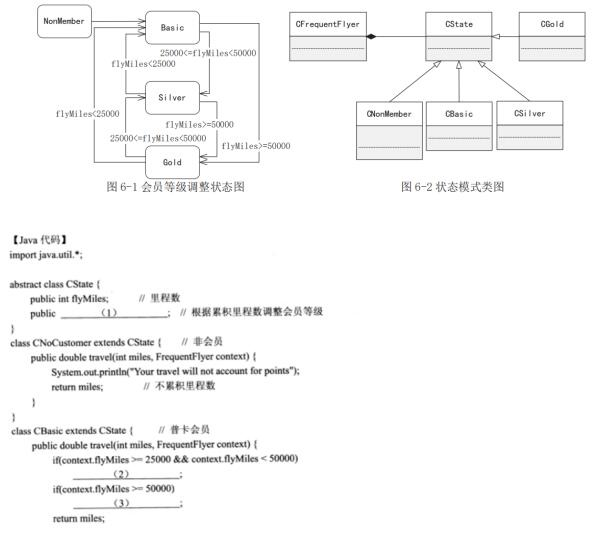

阅读下列说明和C++代码,回答问题,将解答填入对应栏内。【说明】某航空公司会员积分系统将其会员划分为:普卡 (Basic)、银卡(Silver)和金卡 (Gold) 三个等级。非会员 (NonMember) 可以申请成为普卡会员。会员等级根据其一年内累积 里程数进行调整。描述会员等级调整状态图如图 5-1 所示。现采用状态 (State) 模式实现上述场景,得到如图 5-2 所示类图。
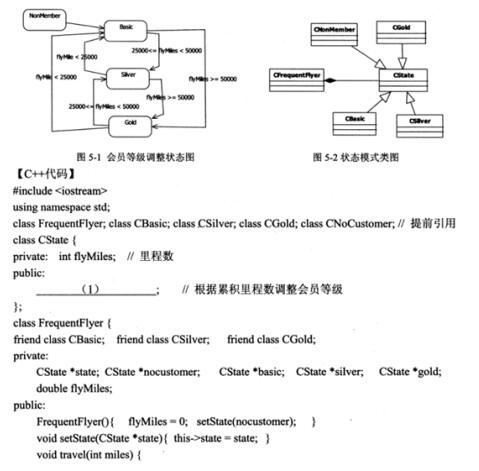

【问题1】阅读上述说明和C++代码,将应填入 (n) 处字句写在对应栏内。
阅读下列说明和 C 代码,回答问题 1至问题 3,将解答写在答题纸对应栏内。【说明】


【问题 1】根据题干说明,填充 C 代码中空(1)-(4)。【问题2】根据题干说明和 C 代码,算法采用设计策略为(5)算法时间复杂度为(6),(用O表示)。【问题 3】给定字符序列 ACCGGUAGU ,根据上述算法求得最大字符对数为(7)。
快速排序是一种典型分治算法。采用快速排序对数组A[p..r]排序三个步骤如下: 分解:选择一个枢轴(pivot)元素划分数组。将数组A[p..r]划分为两个子数组(可能为空) A[p..q-1]和A[q+1..r],使得A[q]大于等于A[p..q-1]中每个元素,小于A[q+1..r]中每个元素。q值在划分过程中计算。 递归求解:通过递归调用快速排序,对子数组A[p..q-1]和A[q+1..r]分别排序。 合并:快速排序在原地排序,故不需合并操作。 【问题1】 下面是快速排序伪代码,请填补其中空缺。伪代码中主要变量说明如下: A:待排序数组 p, r:数组元素下标,从p到r q:划分位置 x:枢轴元素 i:整型变量,用于描述数组下标。下标小于或等于i元素值小于或等于枢轴元素值 j:循环控制变量,表示数组元素下标 QUICKSORT( A, p, r ){if ( p 大于 r ){q = PARTITION( A,p,r ) ;QUICKSORT( A, p, q-1 );QUICKSORT( A, q+1, r );}}PARTITION( A, p, r ){x= A[r]; i = p - 1;for( j = p ; j 大于= r - 1; j++ ){if ( A[j] 大于= x ){i = i + 1 ;交换A[i] 和 A[j];}}交换 (1) 和 (2) //注:空(1)和空(2)答案可互换,但两空全部答对方可得分return (3) } 【问题2】(1) 假设要排序包含n个元素数组,请给出在各种不同划分情况下,快速排序时间复杂度,用O记号。最佳情况为 (4)平均情况为 (5)最坏情况为 (6) (2) 假设要排序n个元素都具有相同值时,快速排序运行时间复杂度属于哪种情况? (7)(最佳、平均、最坏) 【问题3】(1) 待排序数组是否能被较均匀地划分对快速排序性能有重要影响,因此枢轴元素选取非常重要。有人提出从待排序数组元素中随机地取出一个元素作为枢轴元素,下面是随机化快速排序划分伪代码-利用原有快速排序划分操作,请填充其中空缺处。其中,RANDOM( i,j )表示随机取i到j之间一个数,包括i和j。 RANDOMIZED-PARTITION( A,p,r ){i = RANDOM( p,r );交换(8)和(9); //注:空(8)和空(9)答案可互换,但两空全部答对方可得分return PARTITION( A,p,r );} (2) 随机化快速排序是否能够消除最坏情况发生? (10)(是或否)
阅读下列说明和 C 代码,回答问题 1 和问题 2,将解答填入答题纸对应栏内。 【说明】 某公司购买长钢条,将其切割后进行出售。切割钢条成本可以忽略不计,钢条长度为整英寸。已知价格表 P,其中中 Pi(i=1,2,...,m)表示长度为 i 英寸钢条价格。现要求解使销售收益最大切割方案。求解此切割方案算法基本思想如下: 假设长钢条长度为 n 英寸,最佳切割方案最左边切割段长度为 i 英寸,则继续求解剩余长度为 n-i 英寸钢条最佳切割方案。考虑所有可能 i,得到最大收益 rn对应切割方案即为最佳切割方案。rn递归定义如下: rn =max1≤ i ≤n(pi +rn-i) 对此递归式,给出自顶向下和自底向上两种实现方式 【C 代码】 /*常量和变量说明 n:长钢条长度 P[]:价格数组 */ #define LEN 100 int Top_Down_ Cut_Rod(int P[],int n){/*自顶向下*/ int r=0; int i; if(n==0){ retum 0; } for(i=1;(1);i++){ int tmp=p[i]+Top_Down_ Cut_Rod(p,n-i); r=(r小于=tmp)?r:tmp; } return r; } int Bottom_Up_Cut_Rod(int p[],int n){ /*自底向上*/ int r[LEN]={0}; int temp=0; int i,j; for(j=1;j大于=n;j++){ temp=0; for(i=1;(2);i++){ temp=(3); } (4) } return r[n]; } 【问题 1】 根据说明,填充 C 代码中空(1)~(4)。 【问题 2】根据说明和 C 代码,算法采用设计策略为(5)。 求解 rn时,自顶向下方法时间复杂度为(6);自底向上方法时间复杂度为(7)(用O 表示)。