已知函数 f（x） ＝|x﹣ 2|+|x+1|．
（1） 解关于 x 的不等式 f（x） ≤5；
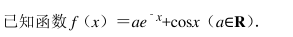
阿基米德（公元前 287 年﹣ 公元前 212 年， 古希腊） 不仅是著名的哲学家、 物理学家， 也是著名的数学家， 他利用“逼近法” 得到椭圆的面积除以圆周率 π 等于椭圆的长半轴长与短半轴长的乘积． 在平面直角坐标系 Oxy 中， 椭圆 C：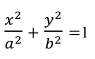
（a＞b＞0） 的面积为 2√3π， 两焦点与短轴的一个顶点构成等边三角形． 过点（1， 0） 的直线l 与椭圆 C 交于不同的两点 A， B．
（1） 求椭圆 C 的标准方程；
（2） 设椭圆 C 的左、 右顶点分别为 P， Q， 直线 PA 与直线 x＝4 交于点 F， 试证明 B， Q，F 三点共线；
（3） 求△AOB 面积的最大值．
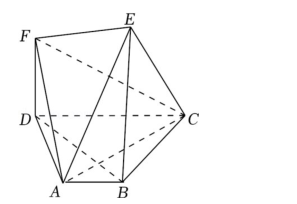
如图， 在多面体 EFABCD 中， AB∥CD， AB⊥BC， EB⊥平面 ABCD， BE∥DF，CD＝2BC＝4AB＝4， BE＝2DF＝4．
（Ⅰ ） 求证： AC⊥EF；
（Ⅱ ） 求三棱锥 A﹣ CDF 的体积．
在△ABC 中， a， b， c 分别是内角 A， B， C 的对边， 且（a+c）2 ＝b 2 +3ac．
（Ⅰ ） 求角 B 的大小；
（Ⅱ ） 若 b＝2， 且 sinB+sin（C﹣ A） ＝2sin2A， 求△ABC 的面积．
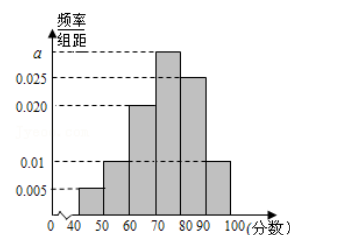
某校从高一年级学生中随机抽取 40 名学生， 将他们的期中考试数学成绩（满分 100 分， 成绩均为不低于 40 分的整数） 分成六段： [40， 50）， [50， 60）， …， [90， 100]后得到如图的频率分布直方图．
（1） 求图中实数 a 的值；
（2） 若该校高一年级共有学生 1000 人， 试估计该校高一年级期中考试数学成绩不低于60 分的人数．
（3） 若从样本中数学成绩在[40， 50） 与[90， 100]两个分数段内的学生中随机选取 2 名学生， 试用列举法求这 2 名学生的数学成绩之差的绝对值大于 10 的概率．
