当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->案例:下面是高中“直线与圆的位置关系”一节的部分教材内容。问
案例:下面是高中“直线与圆的位置关系”一节的部分教材内容。


问题:
(1)阅读这段教材,概括与圆相关的知识点;
(2)阅读这段教材中的思考,说明设置此栏目内容的主要意图;
(3)请说明圆与方程这一章内容在高中数学课程中的地位和作用。
(1)①平面上直线与圆有三种位置关系:
当圆心到直线的距离小于半径时,直线与圆相交;
当圆心到直线的距离等于半径时,直线与圆相切;
当圆心到直线的距离大于半径时,直线与圆相离。
②圆的标准方程为(x-a)2+(y-b)2=r2(r>0),其中圆心是c(a,b),半径为r;
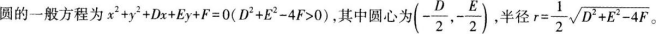
③已知直线方程Ax+By+C=0与圆方程(x-a)2+(y-b)2=r2(r>O),判断直线与圆位置关系的方法。

圆与直线相切时:d=r;
圆与直线相离时:d>r。
代数法:联立直线与圆的方程,转化为一元二次方程,用判别式A判断。
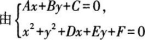
消元,得到一元二次方程的判别式△,当
△>0时,圆与直线相交;
△=0时,圆与直线相切;
△<0时,圆与直线相离。
(2)通过设置思考栏目,引导学生回顾初中有关直线与圆位置关系的相关知识,促使学生将之前所学的知识与现阶段学习的解析几何知识联系起来,有助于学生构建清晰的知识脉络,理解各知识点之间的关联性。明晰相同点和不同点,从而在解决数学问题时可以做到~题多解,举一反三。
(3)根据《普通高中数学课程标准(2017年版)》的理念,高中数学课程要以学生发展为本,注重培养学生的科学精神和创新意识,提升学生数学学科的核心素养,为学生进一步学习和获得较高的数学素养打下基础。“圆与方程”这一章介于“直线与方程”“圆锥曲线”这两章之间,先学习“直线与方程”便于学生在知识体系上过渡到“圆与方程”的学习,从而学生得以掌握研究平面几何图形基本的探究方法和思维方式,为之后选修科目中“椭圆方程”的学习打下基础。同时圆作为生活中极为常见的几何图形,让学生利用数学方法研究圆,有助于学生能够更客观地认识生活中的圆,所以本章节的学习在高中数学的学习中起到一个承上启下的作用。
圆的教学在平面几何中乃至整个中学教学中都占有重要的地位,本章利用解析几何的方法对初中学习的圆的相关知识进行深化研究,帮助学生在平面直角坐标系中,认识直线、圆的相关几何特征,感悟平面解析几何中蕴含的数学思想。本章的教学符合《普通高中数学课程标准(2017年版)》的基本理念,有助于培养学生的探索精神,提升学生的数学素养。
有“泥土诗人”之称的诗人是()。
将下列各项按所表示年龄大小顺序排列,正确的顺序应是( )。
①不惑②垂髫③花甲④加冠⑤而立⑥古稀⑦半百
钱穆在评论中国古代某制度时说,它“可以培植全国人民对政治之兴味……可以团结全国各地域于一个中央之统治”,这一制度是()。
明朝初年强化君主专制的措施是()。
1931年,一位给人们带来光明的科学家重病的消息牵动着世界人民的心,几十名记者为他守夜。每隔一个小时就对外发布一次消息:“灯”还亮着。这位科学家是( )。
在我国历史上,传统音乐与外族音乐、北方与南方音乐进行广泛交流的时期是()。
下列哪部歌剧是瓦格纳的作品()
乐器“缶”的制作材料属于( )。
隋唐至宋,在宫廷宴饮时娱乐欣赏的音乐称为()。
双簧管属于()。