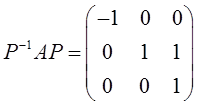设A为3阶矩阵,α1,α2为A的分别属于-1,1的特征向量,向量α3满足Aα3=α2+α3。
(Ⅰ)证明α1,α2,α3线性无关;
(Ⅱ)令P=(α1,α2,α3),求P-1AP。
证明:(Ⅰ)设存在数k1,k2,k3,使得k1α1+k2α2+k3α3=0①。
由已知条件知Aα1=-α1,Aα2=α2。用矩阵A分别乘式①的左右两边,得-k1α1+k2α2+k3(α2+α3)=0②。
式①-②得2k1α1-k3α2=0。
由于α1,α2为A的分别属于-1,1的特征向量,所以α1,α2线性无关,即k1=k3=0,代入①得k2α2=0。
因为α2是A的特征向量,α2≠0,得k2=0,即k1=k2=k3=0,所以α1,α2,α3线性无关。
(Ⅱ)由题意有
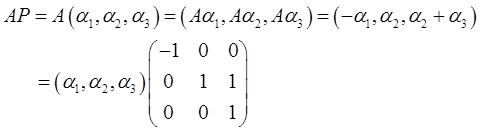
因为α1,α2,α3线性无关,所以矩阵P可逆,得