设n元线性方程组Ax=b,其中
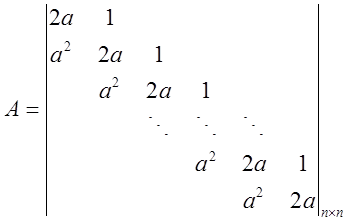
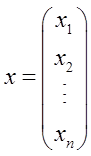
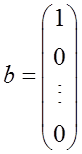
(Ⅰ)证明行列式|A|=(n+1)an;
(Ⅱ)当a为何值时,该方程组有唯一解,并求x1;
(Ⅲ)当a为何值时,该方程组有无穷多解,并求其通解。
证明:(Ⅰ)方法一:数学归纳法
记
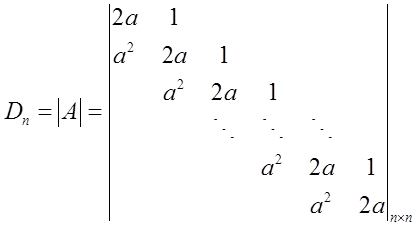
以下用数学归纳法证明Dn=(n+1)an。
当n=1时,D1=2a,结论成立;
当n=2时,
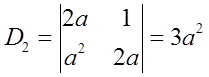
结论成立;
假设结论对小于n的情况成立。将Dn按第一行展开得
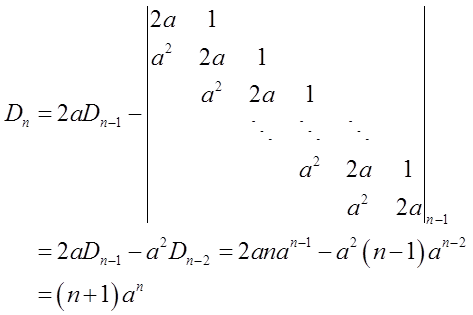
故|A|=(n+1)an。
方法二:消元法
记
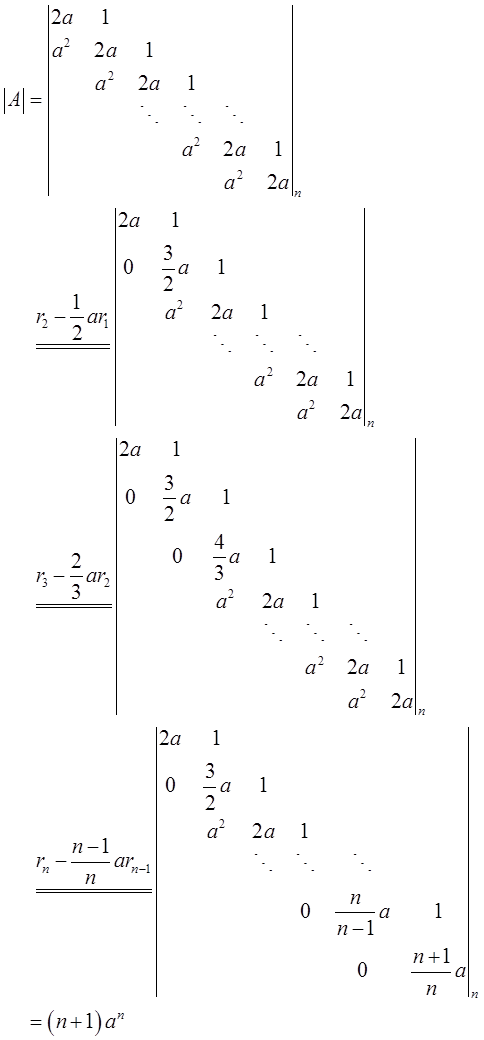
(Ⅱ)当a≠0时,方程组系数行列式Dn≠0,故方程组有唯一解。由克莱姆法则,将Dn得第一列换成b,得行列式为
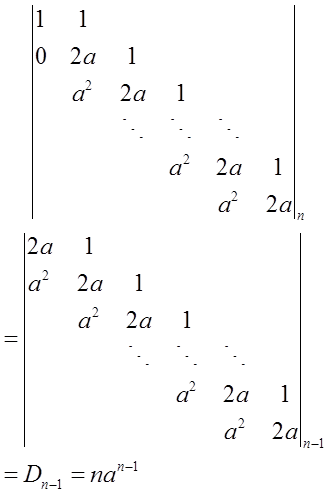
所以,当a≠0时,有唯一解
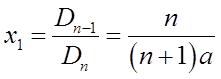
(Ⅲ)当a=0时,方程组为
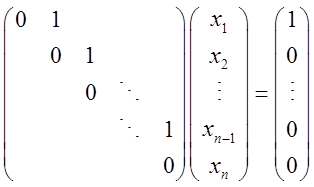
此时方程组系数矩阵得秩和增广矩阵的秩均为n-1,所以方程组有无穷多组解,其通解为x=(0,1,0,…,0)T+k(1,0,…,0)T,其中k为任意常数。