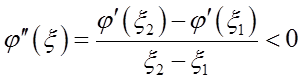(Ⅰ)证明积分中值定理:若函数f(x)在闭区间[a,b]上连续,则至少存在一点η∈[a,b],使得
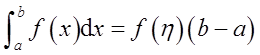
(Ⅱ)若函数φ(x)具有二阶导数,且满足φ(2)>φ(1),
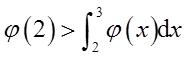
则至少存在一点ξ∈(1,3),使得φ″(ξ)<0。
证明:(Ⅰ)若函数f(x)在闭区间[a,b]上连续,则必存在最大值M和最小值m,即m≤f(x)≤M,x∈[a,b]。
于是有
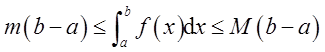
即
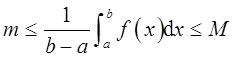
根据闭区间上连续函数的介值定理,在[a,b]上至少存在一点η∈[a,b],使得
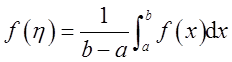
因此而得证。
(Ⅱ)根据(Ⅰ)中结论可得,存在η∈[2,3],使得
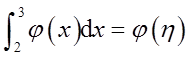
由
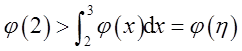
知η∈[2,3]。
由φ(2)>φ(1),利用微分中值定理,存在ξ1∈(1,2),使得
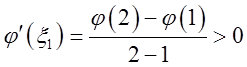
由φ(2)>φ(η),利用微分中值定理,存在ξ2∈(2,η),使得
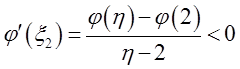
存在ξ∈(ξ1,ξ2)?(1,3),使得