厂商如何生产才能实现最小成本?
(l)厂商在既定产量下实现最小成本的条件是:MRTSLK=w/r,即生产要素的边际技术替代率正好等于它们的价格之比。 (2)具体分析如图4-3所示。图4-3中有一条等产量曲线Q和三条等成本线AB、A’B’,和A”B”。唯一的等产量曲线Q代表既定的产量。三条等成本线具有相同的斜率(即表示两要素的价格是既定的),但代表三个不同的成本量,其中,等成本线AB代表的成本大于等成本线A’B’,等成本线A’B’代表的成本大于等成本线A”B”。唯一的等产量曲线Q与其中一条等成本线A’B’相切于E点,这就是生产的均衡点或最优要素组合点。它表示在既定的产量条件下,生产者应该选择E点的要素组合(OK1,OL1)才能实现最小的成本。 这是因为,等成本线A”B”虽然代表的成本较低,但它与既定的等产量曲线Q既无交点又无切点,它无法实现等产量曲线Q所代表的产量。等成本曲线AB虽然与既定的等产量曲线Q相交于a、b两点,但它代表的成本过高,通过沿着等产量曲线Q由a点向E点或由6点向E点的移动,都可以获得相同的产量而使成本下降。所以只有在切点E才是在既定产量条件下实现最小成本的要素组合。 再进一步具体地分析等产量曲线Q与等成本线AB的两个交点a点和b点。 如果厂商开始时在a点进行生产。由图4-3可见,a点等产量曲线的斜率的绝对值大于等成本线的斜率的绝对值,它表示在a点上的两要素的边际技术替代率大于两要素的价格之比。例如,
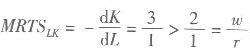
时,根据不等式的左边,在生产过程中,在维持产量水平不变的前提下,厂商可以用l单位的劳动去替代3单位的资本(因为
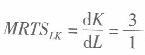
)。而根据不等式的右边,在生产要素市场上,3单位资本的购买成本却可以购买到1.5单位的劳动(因为
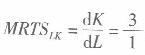
)。于是,厂商因节省0.5单位劳动的购买成本而得利。 对b点的分析与之正好相反。 由此可见,只要MRTSLK>w/r,厂商就会不断地用劳动去替代资本,即在图4-3中沿着等产量曲线Q由a点不断向E点靠近;只要MRTSLK